Задача №52.
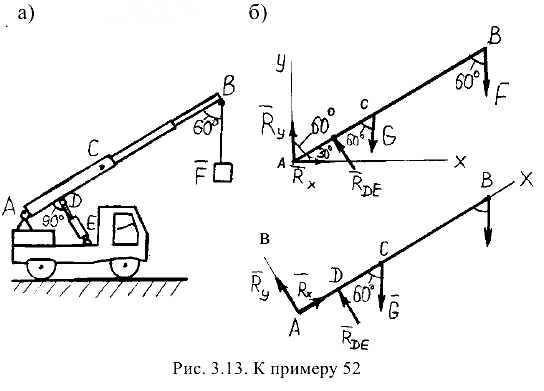
Телескопическая стрела 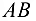 автокрана (рис. 3.13, а) весом
автокрана (рис. 3.13, а) весом 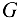 = 4 кН с центром тяжести в точке
= 4 кН с центром тяжести в точке 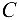 песет на конце груз
песет на конце груз 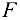 = 15 кН. Стрела удерживается в равновесии с помощью гидравлического домкрата
= 15 кН. Стрела удерживается в равновесии с помощью гидравлического домкрата 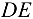 . Принимая
. Принимая
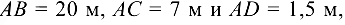
определить реакции опорного шарнира 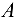 и силу, нагружающую шток домкрата.
и силу, нагружающую шток домкрата.
Решение:
Рассматриваем равновесие стрелы 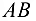 . К ней приложены заданные активные силы — вес груза
. К ней приложены заданные активные силы — вес груза 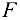 и вес стрелы
и вес стрелы 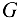 . Рассматривая тело
. Рассматривая тело 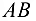 как свободное, отбрасываем связи (стержень домкрата
как свободное, отбрасываем связи (стержень домкрата 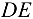 и шарнирно-неподвижную опору
и шарнирно-неподвижную опору 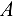 ), заменяя их действие реакциями. Реакция
), заменяя их действие реакциями. Реакция 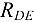 стержня направлена вдоль него к телу
стержня направлена вдоль него к телу 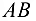 (так как очевидно, что в нашем случае стержень сжат). Реакция опоры
(так как очевидно, что в нашем случае стержень сжат). Реакция опоры 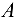 заранее по направлению неизвестна, поэтому заменяем ее двумя составляющими
заранее по направлению неизвестна, поэтому заменяем ее двумя составляющими 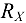 и
и 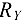 по осям координат, принимая обычное вертикально-горизонтальное направление координатных осей. Расчетная схема изображена на рис. 3.13, б. Для полученной плоской произвольной системы сил составляем три уравнения равновесия (напоминаем, что в качестве центра моментов целесообразно выбирать точку пересечения двух неизвестных сил — в нашем случае точку
по осям координат, принимая обычное вертикально-горизонтальное направление координатных осей. Расчетная схема изображена на рис. 3.13, б. Для полученной плоской произвольной системы сил составляем три уравнения равновесия (напоминаем, что в качестве центра моментов целесообразно выбирать точку пересечения двух неизвестных сил — в нашем случае точку 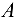 ):
):

Составляем проверочное уравнение равновесия, в качестве которого может быть принято любое уравнение проекций или моментов, кроме уже использованных в решении. Возьмем, например

Полученное небольшое расхождение в третьем знаке допустимо, так как объясняется погрешностью счета. Следовательно, реакции 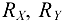 и
и 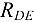 определены верно. Реакция
определены верно. Реакция 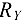 получилась отрицательной; это указывает на то, что ее действительное направление противоположно предварительно выбранному. Искомая сила, нагружающая шток домкрата
получилась отрицательной; это указывает на то, что ее действительное направление противоположно предварительно выбранному. Искомая сила, нагружающая шток домкрата 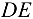 , по модулю равна найденной реакции, а по направлению противоположна ей.
, по модулю равна найденной реакции, а по направлению противоположна ей.
В двух из трех уравнений равновесия, использованных в решении, содержалось более чем по одному из неизвестных, чего можно было избежать, направив координатные оси по-другому (рис. 3.13, в). При этом уже две точки (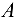 и
и 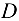 ) будут точками пересечения двух неизвестных сил (так как изменилось направление составляющих реакций опоры
) будут точками пересечения двух неизвестных сил (так как изменилось направление составляющих реакций опоры 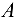 ), что позволит применить другую систему уравнений равновесия:
), что позволит применить другую систему уравнений равновесия:
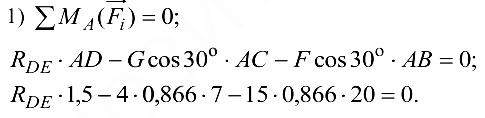
Это уравнение осталось без изменений. Получаем
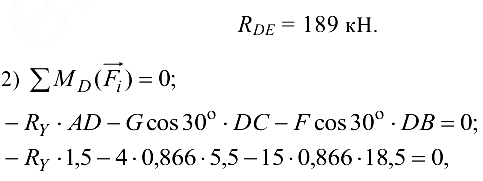
отсюда
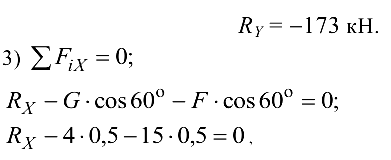
отсюда
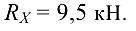
Составляем проверочное уравнение равновесия:
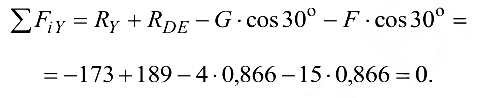
Во втором варианте решения иным направлениям составляющих реакций 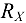 и
и 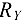 опоры
опоры 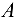 соответствуют и иные их значения. Полная реакция опоры
соответствуют и иные их значения. Полная реакция опоры 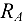 не зависит от направления ее составляющих, в чем легко убедиться с помощью расчета:
не зависит от направления ее составляющих, в чем легко убедиться с помощью расчета:
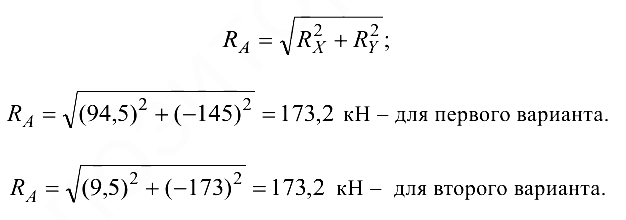
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

