Задача №21.
Пример имеет своим прототипом схему по расчёту усилий в раскосах и поясах мачтовых опор ЛЭП.
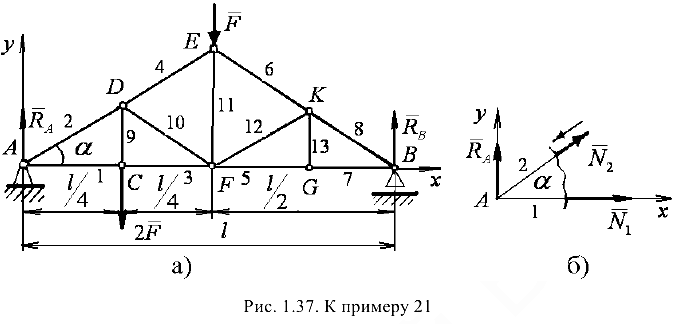
Для фермы (рис. 1.37, а) определить усилия в стержнях, если в узле 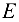 приложена сила
приложена сила 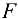 = 1800 Н, в узле
= 1800 Н, в узле 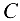 — сила 2
— сила 2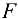 , а угол
, а угол 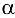 = 37°
= 37°
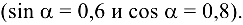
Размеры стержня указаны на чертеже.
Решение:
Освобождаемся от связей, заменяя их реакциями опор. На ферму действует плоская система произвольно расположенных сил. Реакции опор соответственно будут
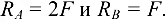
Применяя лемму 2 о пулевых стержнях плоской фермы сначала к узлу 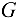 , а затем к узлу
, а затем к узлу 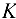 , находим, что
, находим, что
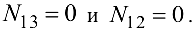
Обратимся к определению усилий в стержнях фермы способом вырезания узлов. Определение усилий начинают с узла, в котором сходятся только два стержня (узлы 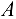 и
и 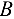 ). В дальнейшем выбирают такие узлы фермы, в которых также будут неизвестными два усилия, и так до тех пор, пока не будут определены усилия во всех стержнях фермы.
). В дальнейшем выбирают такие узлы фермы, в которых также будут неизвестными два усилия, и так до тех пор, пока не будут определены усилия во всех стержнях фермы.
Узел 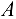 . Вырезав узел (рис. 1.37, б), приложим к нему неизвестные усилия
. Вырезав узел (рис. 1.37, б), приложим к нему неизвестные усилия 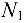 (в стержне 1),
(в стержне 1), 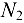 (в стержне 2) и реакцию опоры в точке
(в стержне 2) и реакцию опоры в точке 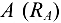 . В итоге на узел действует плоская система трех сходящихся сил. Для определения неизвестных усилий
. В итоге на узел действует плоская система трех сходящихся сил. Для определения неизвестных усилий 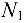 и
и 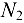 составим уравнения равновесия
составим уравнения равновесия
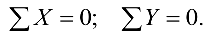
Неизвестные усилия будем всегда принимать растягивающими -усилия направлены от узла. Если в результате вычисления усилие окажется отрицательным, то принятое направление усилия следует заменить па обратное (сжатие).
Выберем систему координат через точку 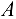 так, чтобы ось
так, чтобы ось 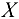 совпадала с линией действия усилия
совпадала с линией действия усилия 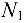 . В этом случае уравнения равновесия принимают вид
. В этом случае уравнения равновесия принимают вид
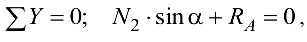
откуда
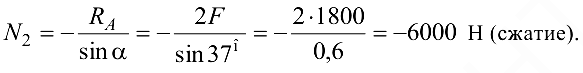
Знак «минус» для усилия 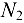 указывает на то, что стержень не растянут, а сжат (следует изменить на рис. 1.37, б направление усилия
указывает на то, что стержень не растянут, а сжат (следует изменить на рис. 1.37, б направление усилия 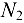 ). После этого изменения уравнение
). После этого изменения уравнение 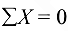 принимает вид
принимает вид
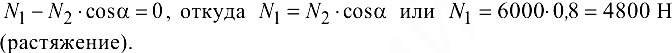
Узел 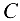 . Вырезав узел (рис. 1.38, а), приложим к нему неизвестные усилия
. Вырезав узел (рис. 1.38, а), приложим к нему неизвестные усилия 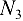 (в стержне 3) и
(в стержне 3) и 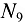 (в стержне 9). В итоге в узле
(в стержне 9). В итоге в узле 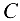 действует плоская система четырех сходящихся сил, из которых неизвестными усилиями являются
действует плоская система четырех сходящихся сил, из которых неизвестными усилиями являются 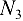 и
и 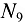 . Выбрав через точку
. Выбрав через точку 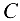 систему координат
систему координат 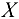 и
и 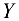 , напишем уравнения равновесия:
, напишем уравнения равновесия:
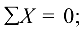
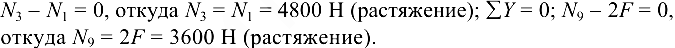
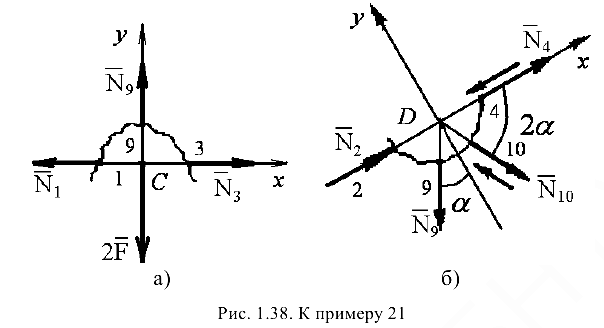
Узел 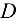 . Вырезав узел (рис. 1.38, б), приложим к нему неизвестные усилия
. Вырезав узел (рис. 1.38, б), приложим к нему неизвестные усилия 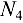 (в стержне 4) и
(в стержне 4) и 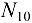 (в стержне 10). В итоге в узле
(в стержне 10). В итоге в узле 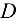 действует плоская система четырех сходящихся сил, из которых неизвестными являются усилия
действует плоская система четырех сходящихся сил, из которых неизвестными являются усилия 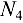 и
и 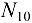 .
.
Проведем через точку 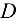 систему координат
систему координат 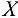 и
и 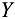 так, чтобы ось
так, чтобы ось 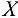 проходила по стержню 4. Уравнения равновесия принимают вид
проходила по стержню 4. Уравнения равновесия принимают вид
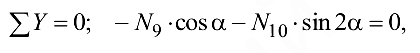
или
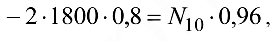
или
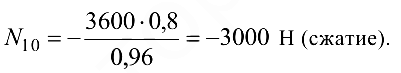
Направление усилия 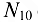 следует изменить на обратное (рис. 1.38, б).
следует изменить на обратное (рис. 1.38, б).
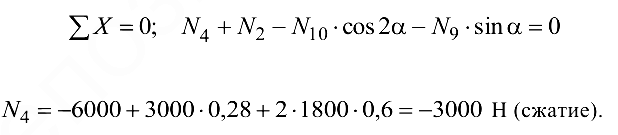
Направление усилия 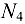 также следует изменить на обратное (рис. 1.38, б).
также следует изменить на обратное (рис. 1.38, б).
Узел 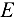 . Вырезав узел (рис. 1.39, а), приложим к нему неизвестные усилия
. Вырезав узел (рис. 1.39, а), приложим к нему неизвестные усилия 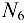 (в стержне 6) и
(в стержне 6) и 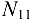 (в стержне 11). В итоге в узле
(в стержне 11). В итоге в узле 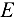 действует плоская система четырех сходящихся сил:
действует плоская система четырех сходящихся сил: 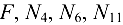 . Через точку
. Через точку 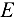 проводим систему координат
проводим систему координат 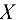 и
и 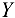 так, чтобы ось
так, чтобы ось 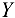 проходила по стержню 11. Составляем уравнения равновесия:
проходила по стержню 11. Составляем уравнения равновесия:
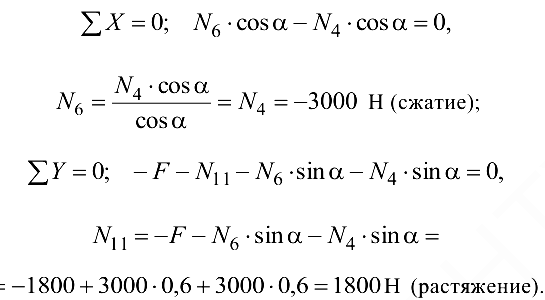
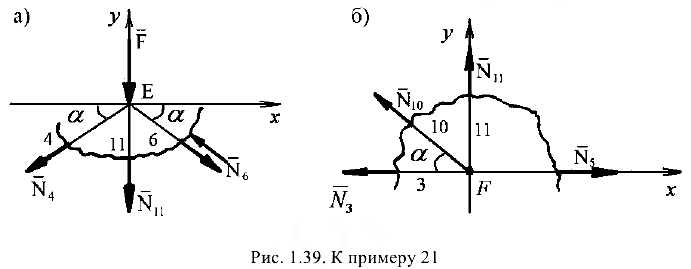
Усилие 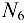 следует направить в обратную сторону (см. рис. 1.39, а). Узел
следует направить в обратную сторону (см. рис. 1.39, а). Узел 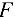 . Вырезав узел (рис. 1.39, б), приложим к нему неизвестное усилие
. Вырезав узел (рис. 1.39, б), приложим к нему неизвестное усилие 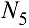 (в стержне 5). В итоге в узле
(в стержне 5). В итоге в узле 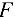 получаем плоскую систему четырех сходящихся сил, из которых неизвестным усилием является
получаем плоскую систему четырех сходящихся сил, из которых неизвестным усилием является 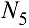 . Проведя через точку
. Проведя через точку 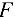 систему координат
систему координат 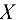 и
и 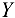 , напишем уравнение равновесия
, напишем уравнение равновесия
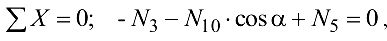
откуда
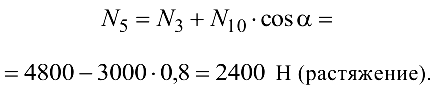
Узел 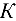 . Вырезав узел (рис. 1.40, а), приложим к нему неизвестное усилие (в стержне 8). В итоге в узле
. Вырезав узел (рис. 1.40, а), приложим к нему неизвестное усилие (в стержне 8). В итоге в узле 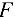 получаем плоскую систему двух сходящихся сил:
получаем плоскую систему двух сходящихся сил: 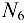 и
и 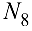 . Через точку
. Через точку 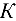 проводим систему координат
проводим систему координат 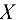 и
и 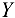 . Составляем уравнение равновесия:
. Составляем уравнение равновесия:
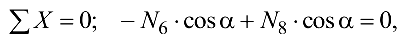
откуда
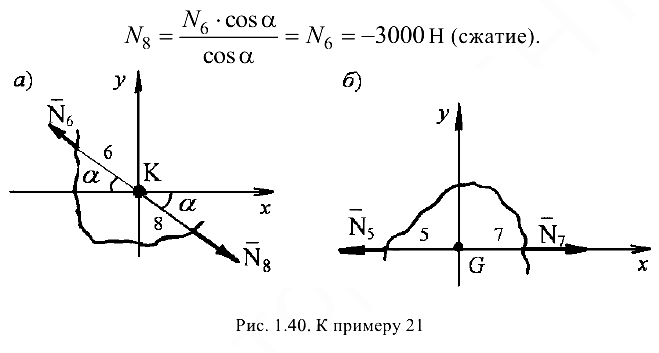
Узел 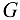 . Вырезав узел (рис. 1.40, б), приложим к нему неизвестное усилие
. Вырезав узел (рис. 1.40, б), приложим к нему неизвестное усилие 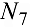 (в стержне 7). В итоге в узле
(в стержне 7). В итоге в узле 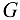 получаем систему двух сходящихся сил с неизвестным усилием
получаем систему двух сходящихся сил с неизвестным усилием 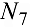 . Выбрав через точку
. Выбрав через точку 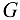 систему координат
систему координат 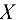 и
и 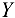 , запишем уравнение равновесия
, запишем уравнение равновесия
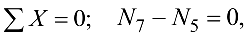
откуда
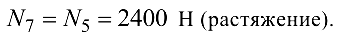
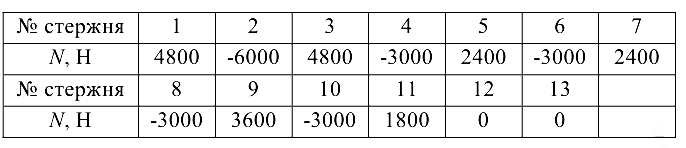
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

