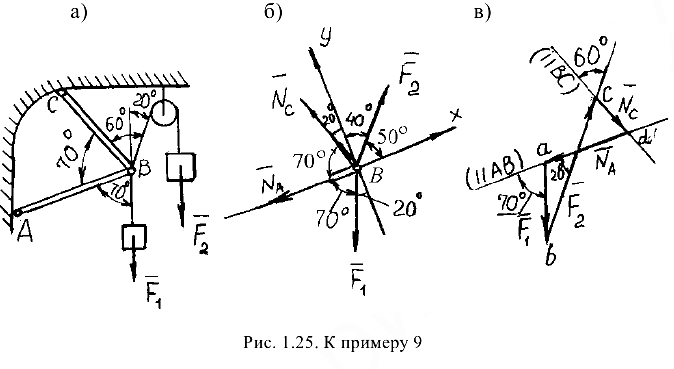
Задача №9.
Определить реакции стержней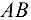 
и 
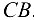, общий шарнир 
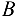которых нагружен, как показано на рис. 1.25, а, силами
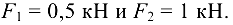
Решение:
- Выделим точку, равновесие которой следует рассмотреть, чтобы определить неизвестные реакции стержней. Здесь такой точкой является шарнир
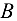. Изобразим его отдельно на рис. 1.25, б. - Изобразим действующие на точку 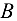активные силы (нагрузки)
и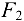 
, действующие па шарнир 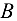вдоль нитей, к которым прикреплен каждый из грузов. - Мысленно освободим шарнир 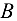от связей (стержней) и заменим действие связей их реакциям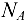и
и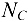 
, направленными вдоль стержне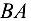й 
и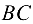 
соответственно. Не всегда заранее можно определить, какой из стержней растянут или сжат. Например, в данном случае груз 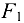сжимает стержень 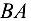и растягивает стержень 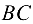, а груз 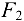— наоборот: растягивает стержень 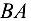и сжимает стержень 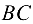. Поэтому существует общепринятое правило считать предположительно все стержни растянутыми. В соответствии с этим правилом реакци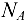и и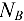 
стержней на рис. 1.25, б направлены от шарнира 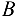к связям. - Приняв точку 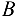за начало координат, выберем положение осей
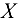(ocь абсцисс) и 
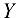(ось ординат) таким образом, чтобы по крайней мере одна из них совпала с линией действия неизвестной силы, т. е. совместив одну из осей координат с осью какого-либо стержня. В данном случае (рис. 1.25, б) ось 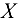совмещена с осью стержня 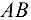(можно было бы ось 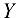совместить с осью стержня 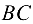). - Определив при помощи данных на рис. 1.25, а углы, образуемые силами
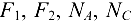с осям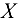и и 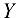, определим проекции всех сил на каждую из осей и составим из этих проекций уравнения равновесия для плоской системы сходящихся сил:
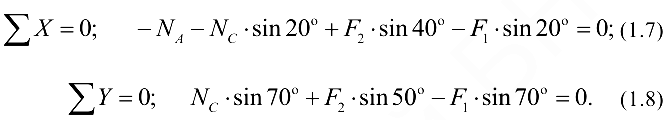
- Решаем получившуюся систему уравнений. Благодаря тому, что ось 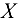совпадает с осью стержня 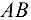, ось 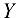перпендикулярна к этому стержню. Проекция 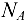(реакция стержня 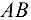) на ось равняется нулю, и второе уравнение содержит только одно неизвестное.
Из уравнения (1.8) имеем
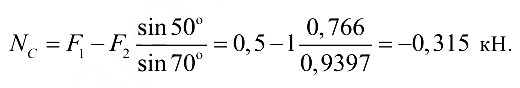
Знак «минус» перед численным значением 
показывает, что вектор (рис. 1.25, б) должен быть направлен в противоположную сторону, т. е. стержень 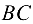не растянут, как предполагалось, а сжат силой 0,315 кН (315 Н).
Из уравнения (1.7) имеем
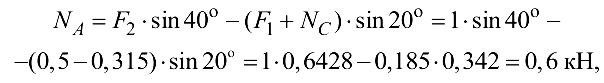
откуда 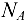= 0,6 кН.
Численное значение 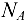положительно, значит, предположительно выбранное направление вектора 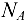соответствует действительному и стержень 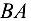растянут силой 0,6 кН (600 Н).
- Решение задачи обязательно следует проверить. Лучшим способом проверки может быть либо решение с помощью иного выбора осей координат (решите эту задачу, совместив ось 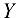с осью стержня 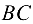), либо решение задачи иным методом, например, графически.
Графическое решение задачи (оно показано на рис. 1.25, в) очень просто выполнять с помощью линейки с миллиметровой шкалой и транспортира. Из произвольной точки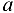 
откладываем вертикально вниз (так направлена сила 
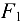) вектор 
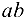, который в некотором масштабе
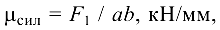
изображает силу 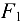. Из точки 
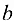параллельно действию силы 
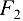на шарнир 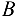в том же масштабе откладываем вектор 
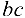, изображающий силу
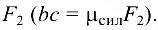
Затем из точек а и с проводим прямые, параллельные соответственно стержню 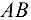и стержню 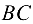. Эти прямые пересекаются в точке 
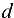. Образовался замкнутый многоугольник 
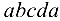, в котором сторона 
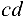изображает реакцию стержня 
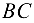, а сторона 
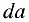— реакцию стержня ( 
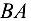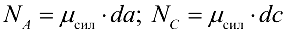). Причем стрелки у этих сторон показывают, который из стержней сжат или растянут.
Ответ:
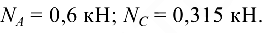
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:
