Задача №3.
Два жестких стержня 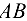 и АС имеют общую шарнирную точку
и АС имеют общую шарнирную точку 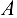 и шарнирные опоры
и шарнирные опоры 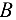 и
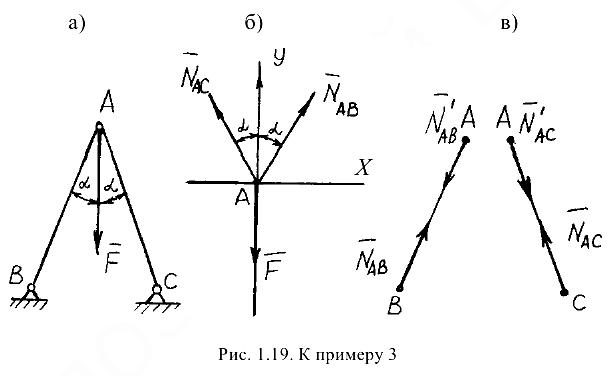
и  (рис. 1.19, а). Сила
(рис. 1.19, а). Сила 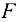 = 500 Н приложена к шарнирному валику в точке
= 500 Н приложена к шарнирному валику в точке 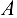 . Стержни
. Стержни 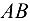 и
и 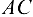 образуют углы
образуют углы 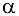 по 30° с линией действия силы
по 30° с линией действия силы 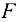 . Определить усилия в стержнях.
. Определить усилия в стержнях.
Решение:
Сила 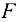 приложена в точке
приложена в точке 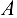 , которая находится в равновесии под действием силы
, которая находится в равновесии под действием силы 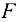 и реакции стержней
и реакции стержней 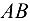 и
и 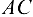 . Реакции стержней направлены вдоль их осей.
. Реакции стержней направлены вдоль их осей.
Рассмотрим равновесие точки 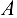 . Отбросив связи точки
. Отбросив связи точки 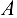 и заменив их реакциями стержней
и заменив их реакциями стержней 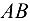 и
и 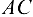 (рис. 1.19, б), получим систему сходящихся сил. Из точки
(рис. 1.19, б), получим систему сходящихся сил. Из точки 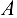 проведём координатные оси. Ось
проведём координатные оси. Ось 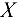 направим перпендикулярно силе
направим перпендикулярно силе 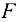 . Составим уравнение равновесия (сумма проекций всех сил на ось
. Составим уравнение равновесия (сумма проекций всех сил на ось 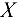 равна нулю):
равна нулю):
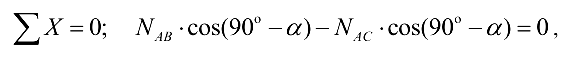
откуда
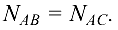
Сумма проекций всех сил на ось 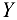 также равна нулю:
также равна нулю:
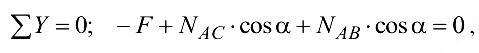
откуда
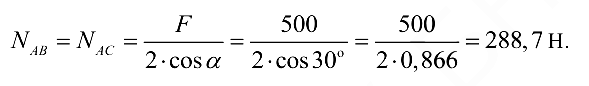
В данном примере силы 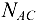 и
и 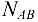 получились со знаком «плюс» (+), следовательно, действительное направление сил совпадает с тем, которое предполагалось при составлении уравнения. Если сила получится со знаком «минус» (-), то это значит, что ее действительное направление противоположно тому, которое было намечено при составлении уравнений равновесия.
получились со знаком «плюс» (+), следовательно, действительное направление сил совпадает с тем, которое предполагалось при составлении уравнения. Если сила получится со знаком «минус» (-), то это значит, что ее действительное направление противоположно тому, которое было намечено при составлении уравнений равновесия.
Мы определили величину, а также направление реакций стержней, приложенных к точке 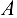 . К верхним концам стержней приложены такие же по величине силы, но противоположно направленные. К нижним концам стержней приложены силы реакции опор
. К верхним концам стержней приложены такие же по величине силы, но противоположно направленные. К нижним концам стержней приложены силы реакции опор 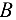 и
и 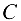 , равные по величине силам, приложенным к верхним концам, и направленные им навстречу (рис. 1.19, в). Следовательно, оба стержня сжимаются силами
, равные по величине силам, приложенным к верхним концам, и направленные им навстречу (рис. 1.19, в). Следовательно, оба стержня сжимаются силами
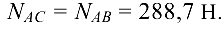
Ответ:
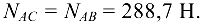
Эта задача с решением взята со страницы решения задач по предмету «прикладная механика»:
Решение задач по прикладной механике
Возможно эти страницы вам будут полезны:

