Кручение стержня круглого поперечного сечения
Цилиндрический брус, закрепленный одним концом и нагруженный парой сил с моментом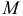 
, действующей в плоскости поперечного сечения бруса, подвергается деформации, называемой кручением. Для изучения этого вида деформации на поверхность круглого резинового стержня наносят сетку из равноотстоящих окружностей и образующих (рис 2.41, а). Если один конец стержня закрепить, а другой нагрузить парой сил, действующей в плоскости, перпендикулярной к оси стержня, то можно заметить, что образующие цилиндра, превращаются в винтовые линии большого шага (рис. 2.41, б), а прямоугольники сетки превращаются в параллелограммы. Это наблюдение позволяет сделать следующие выводы об основных свойствах деформации кручения в пределах упругих деформаций.
- Ось цилиндра, подвергнутого скручиванию, называемая осью кручения, не деформируется.
Нормальные поперечные сечения остаются плоскими, нормальными к оси цилиндра, сохраняют первоначальный диаметр и форму,
- т.е. поперечные сечения цилиндра при кручении поворачиваются как жесткие диски, не претерпевая деформации сдвига в плоскости дисков.
- Равноотстоящие поперечные сечения поворачиваются одно относительно другого на равные углы, т. е. угол поворота поперечных сечений относительно закрепленного конца цилиндра увеличивается пропорционально удалению от этого конца. Угол поворота концевого сечения относительно закрепленного конца называют полным углом закручивания и обозначают через
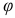. - При кручении цилиндра в его поперечных сечениях возникают только касательные напряжения. Нормальные напряжения в поперечных и продольных сечениях пренебрежимо малы и могут быть приняты равными нулю. В пределах упругих деформаций высоту цилиндра, подвергнутого скручиванию, можно считать неизменной.
Описание процессов, происходящих при деформации кручения, сделано с некоторыми упрощениями, не нарушающими при этом необходимой степени достоверности. Явления, которыми мы пренебрегли, не оказывают существенного влияния на прочность скручиваемых деталей. Однако сделанные допущения позволяют значительно упростить вывод расчетных соотношений. В настоящей главе рассмотрены явления, происходящие при кручении только брусьев круглого поперечного сечения.
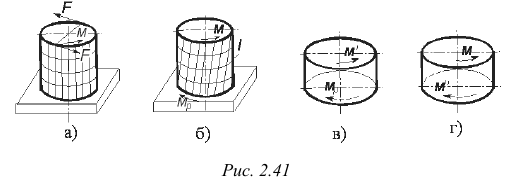
Так как деформация при кручении зависит от величины крутящего момента, действующего в данном сечении, необходимо рассмотреть методику определения крутящего момента в любом сечении цилиндра. В месте закрепления цилиндра (рис. 2.41, б) возникает реактивный крутящий момент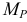 
, равный внешнему крутящему моменту 
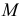, приложенному к свободному концу цилиндра. Рассечем цилиндр плоскостью 
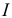и рассмотрим равновесие его нижней части (рис. 2.41, в). Для нахождения нижней части в равновесии необходимо, чтобы момент внутренних сил упругости в данном сечении уравновешивал реактивный момент 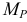, равный :
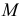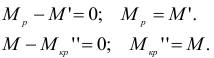
Сопоставляя соотношения (2.72) и (2.73) и принимая во внимание равенство внешнего и реактивного моментов, получаем
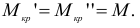
Если отбросить нижнюю часть цилиндра и рассматривать равновесие верхней части, нагруженной моментом 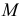, то и в этом случае в сечении 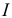возникает момент сил упругости 
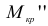равный моменту внешних сил .
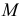Таким образом, крутящий момент, действующий в любом сечении цилиндра, являющийся моментом внутренних сил упругости, численно равен моменту внешней пары сил, действующей по любую сторону от сечения.
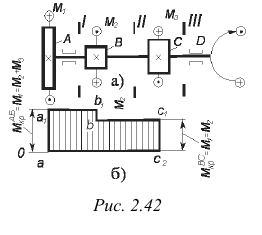
Рассмотрим случай, когда на цилиндр действуют несколько крутящих моментов разного направления. В качестве примера может быть взят ведущий вал редуктора с раздвоенной ступенью (рис. 2.42, а).
На конце вала находится полумуфта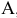 
, к которой приложен крутящий момент 
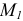, развиваемый двигателем. Между опорами вала расположены два зубчатых колеса 
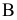и 
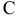, на которые соответственно действуют моменты 
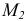и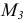 
сопротивления вращению зубчатых колес, находящихся в зацеплении с колесам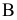и и 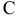. Поэтому момент, развиваемый двигателем, имеет направление, противоположное направлению моментов, приложенных к зубчатым колесам.
При равномерном вращении вала, пренебрегая сопротивлением в подшипниках, имеем
Рассмотрим произвольное сечение вала на участке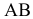 
.
Согласно ранее сказанному, рассматривая левую часть вала, получаем в сечении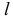 
крутящий момент, уравновешивающий внешний момент 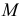, т. е.
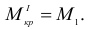
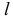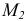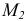Если рассматривать равновесие правой части, то момент в сечении должен уравновесить моменты и или
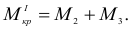
но из соотношения (2.73′)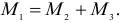 
, что подтверждает равенство правых частей уравнений (2.74) и (2.75).
Аналогично получаем момент в сечении II на участке вала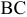 
.
Из равновесия левой части
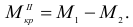
Из равновесия правой части в том же сечении
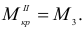
но из соотношения (2.73′)
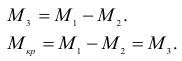
Сечение III (правее точки 
).
Из приведенных выше рассуждений следует, что крутящий момент в любом сечении вала численно равен алгебраической сумме внешних моментов, действующих слева или справа от рассматриваемого сечения в плоскостях, перпендикулярных к оси вала. За положительное направление момента принято такое, при котором внешние моменты, приложенные к валу, вращают отсеченную часть по часовой стрелке, если смотреть со стороны проведенного сечения. В соответствии с этим правилом указаны знаки моментов в соотношениях (2.73′) — (2.79).
Наглядное представление о величине крутящего момента в любом сечении вала дают эпюры крутящих моментов.
Эпюрой крутящих моментов называется диаграмма, изображающая изменение крутящего момента по длине вала (рис. 2.42, б). Методика построения эпюр крутящих моментов сводится к следующему. По ранее установленному правилу определяют величину и знак крутящего момента для характерных участков вала. Проводят горизонтальную прямую 
, именуемую нулевой линией эпюры крутящих моментов. От нулевой линии в выбранном масштабе откладывают ординаты, изображающие величины крутящих моментов: положительные — вверх, отрицательные — вниз. Ломаная 
и представляет собой эпюру крутящих моментов для рассматриваемого случая. Площадь, очерченная эпюрой, покрывается вертикальной штриховкой.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Напряжения при изгибе. Расчеты на прочность |
| Чистый сдвиг и его особенности |
| Напряженное состояние и разрушение при кручении |
| Расчеты на прочность и жесткость |
