Чистый сдвиг и его особенности
Чистым сдвигом называют такое напряженное состояние, когда на гранях элементарного, выделенного из бруса элемента действуют только касательные напряжения. Такие грани называют площадками чистого сдвига.
Пусть, например, к брусу приложены перпендикулярно его оси две равные по модулю, но противоположно направленные силы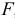 
, действующие весьма близко друг от друга (рис. 2.38, а). При достаточной величине этих сил произойдет срез — отделение левой части бруса от правой по некоторому сечению 
.
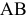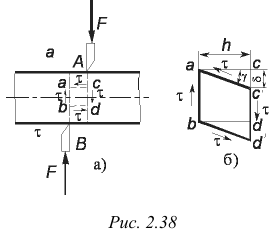
Деформации среза в зоне действия усилий предшествует перекашивание прямых углов параллелепипеда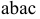 
(рис. 2.38, б). Эту деформацию называют сдвигом. На гранях параллелепипеда возникают касательные напряжения, направление которых определяется законом парности касательных напряжений. Величина касательного напряжения
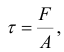
где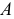 
— площадь поперечного сечения бруса.
Фактически распределение касательных напряжений по сечению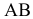 
не является равномерным. Касательные напряжения в узких краевых зонах приближаются к нулю. Однако это обстоятельство при практических расчетах можно не принимать во внимание, так как оно относится к числу местных отклонений и область этих отклонений мала по сравнению с общими размерами сечения.
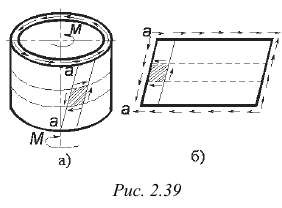
Другим примером, иллюстрирующим состояние чистого сдвига, может служить скручивание тонкостенной трубки (рис. 2.39, а). Под действием внешних моментов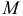 
концевые сечения трубы совершают относительный поворот, вследствие чего стенки трубы испытывают деформацию сдвига, а ее образующие наклоняются. Разрезав мысленно трубу по одной из образующих и развернув ее, увидим, что труба представляет собой пластинку, подверженную чистому сдвигу (рис2.39, б).
Исследуем напряженное состояние при чистом сдвиге с помощью формул (2.19) и (2.20). В этих формулах нормальные напряжения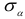 
и 
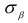на площадках чистого сдвига равны нулю. Это имеет место при 
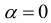или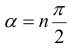 
.
Анализ указанных зависимостей показывает, что при чистом сдвиге главные напряжения равны по величине и противоположны по направлению: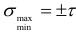 
.
Таким образом, при чистом сдвиге наблюдается «закон парности нормальных напряжений», по форме аналогичный закону парности касательных напряжений. На взаимно перпендикулярных площадках действуют главные напряжения, равные по величине, но имеющие противоположный знак.
Сдвиг является частным случаем двухосного напряженного состояния, так как два главных напряжения не равны нулю.
Из выведенных ранее формул, следует, что главные площадки составляют с площадками чистого сдвига угол 45° и располагаются так, как показано на рис. 2.40.
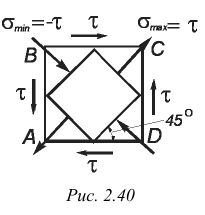
Рассмотрим характерные особенности деформации при сдвиге (см. рис. 2.38, б).
Под действием касательных напряжений грань ей смещается относительно грани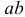 
вниз и занимает новое положение 
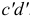. Величина 
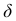сдвига 
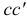относительно плоскости 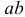носит название абсолютного или линейного сдвига. Величина абсолютного сдвига зависит от расстояния между параллельными плоскостями. Величину 
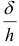называют относительным, сдвигом. Угол 
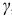у, на который поворачиваются сечения 
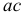и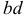 
в процессе деформации, носит название угла сдвига. Угол сдвига в пределах упругой деформации очень мал, поэтому тангенс угла может быть заменен самим углом:
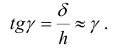
Следовательно, угол сдвига 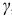характеризует относительную деформацию при сдвиге.
Для деформации чистого сдвига закон Гука выражается соотношением
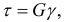
где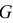 
— коэффициент пропорциональности, называемый модулем упругости второго рода; 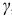— относительный сдвиг.
Модуль упругости второго рода имеет размерность напряжения, так как относительный сдвиг является величиной безразмерной. Величины модулей упругости первого и второго рода связаны следующей формулой, вывод которой здесь не приводится:
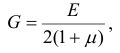
где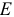 
— модуль упругости первого рода; 
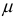— коэффициент Пуассона.
Отметим, что модуль упругости второго рода для стали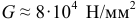 
, для алюминия 
.
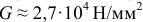Подставив в формулу (2.68) значение касательного напряжения по уравнению (2.66) и относительный сдвиг по выражению (2.67), получим еще один вариант формулы закона Гука для сдвига:
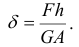
Конструкцию на прочность при деформации сдвига рассчитывают так, чтобы действительные касательные напряжения были меньше допускаемых.
Условие прочности при срезе имеет вид
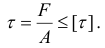
Допускаемое напряжение при срезе обычно принимается как некоторая часть допускаемого напряжения того же материала при растяжении. Для стали, меди и алюминия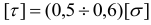 
; для чугуна можно принимать 
.
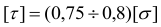Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Геометрические характеристики плоских сечений |
| Напряжения при изгибе. Расчеты на прочность |
| Расчеты на прочность и жесткость |
| Кручение стержня круглого поперечного сечения |
