Напряжения в наклонных площадках при плоском и объемном напряженных состояниях. Обобщенный закон Гука
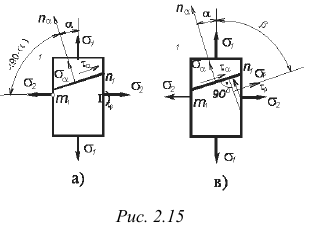
Рассмотрим элемент (рис. 2.15, а), по граням которого действуют растягивающие напряжения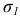 
и 
.
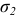Проведем сечение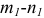 
(перпендикулярно плоскости чертежа), определяющее положение 
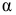-площадки. Напряжения 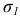и 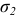вызывают появление на этой площадке напряжени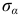й 
и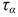 
.
Используя принцип независимости действия сил, можно записать
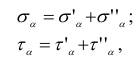
где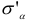 
и 
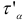— напряжения, вызванные действием 
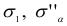и 
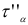— напряжения, вызванные действием .
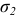Для определения 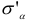и 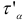воспользуемся формулами (2.12) и (2.13), т. е.
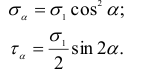
Чтобы получить выражение для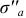 
и 
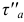в указанные формулы вместо 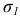необходимо подставить напряжение 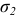, а вместо 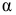-со знаком минус угол 
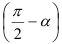который образует нормаль 
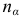с направлением 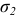. Тогда
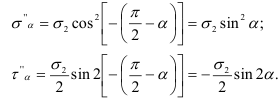
С учетом полученных зависимостей равенства (2.16) и (2.17) принимают следующий вид:
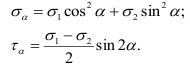
Из формулы (2.19) видно, что максимальные касательные напряжения равны полуразности главных напряжений:
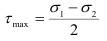
и действуют в площадках, наклоненных под углом 45° к главным площадкам. Экстремальными значениями для нормальных напряжений 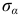согласно зависимости (2.18) будут величины главных напряжений, причем
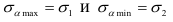
Используя формулы (2.18) и (2.19), определим напряжения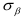 
и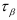 
, действующие по 
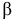-площадке, перпендикулярной к 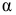-площадке (рис. 2.15, б). По аналогии с изложенным в предыдущем параграфе, окончательно получим
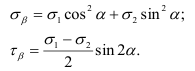
Обратим внимание на следующие два частных случая плоского напряженного состояния.
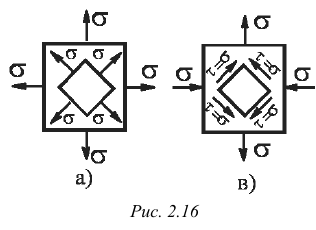
Если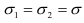 
(рис. 2.16, а), то на всех площадках, проходящих через рассматриваемую точку, нормальное напряжение равно 
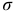, а касательное напряжение отсутствует. Такое напряженное состояние называют равномерным двухосным растяжением (или сжатием).
Если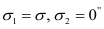 
, а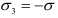 
(рис. 2.16, б), то при 
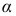= 45° нормальное напряжение в наклонной площадке оказывается равным нулю, а 
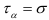. Такое напряженное состояние называют чистым сдвигом.
Совокупность формул (2.18) — (2.21) дает возможность решать прямую задачу плоского напряженного состояния, т. е. по известным главным напряжениям находить нормальные и касательные напряжения в наклонных площадках. При этом следует иметь в виду, что угол 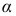всегда отсчитывают от направления алгебраически большего главного напряжения (отличного от нуля), а значения главных напряжений подставляют в эти формулы со своими знаками. Последнее замечание указывает на возможность изменения индексов у главных напряжений в расчетных формулах, поэтому необходимо четко помнить правило их обозначения.
На практике чаще приходится иметь дело с обратной задачей, в которой известными величинами являются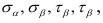 
, а определить необходимо значения главных напряжений и положение главных площадок.
Расчетные формулы для обратной задачи находят из выражений (2.18) — (2.21), если в них предварительно заменить 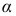на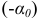 
. Здесь 
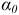-угол, на который необходимо повернуть нормаль па, чтобы получить направление 
.
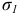Опуская промежуточные выкладки, приведем расчетные формулы в окончательном виде:
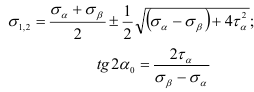
Из выражения (2.23) определяют два значения угла 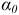, отличающиеся друг от друга на 90°: одно значение угла соответствует площадке, по которой действует максимальное главное напряжение, а другое -площадке с минимальным главным напряжением.
В случае объемного напряженного состояния напряжения по наклонным площадкам, не параллельным ни одному из главных напряжений, определяются по следующим формулам:
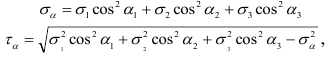
где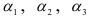 
— углы, которые образует нормаль к рассматриваемой площадке соответственно с направлениями 
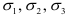. Максимальное касательное напряжение действует по площадке, параллельной главному напряжению 
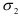и составляющей угол 45° с направлениям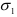и 
и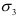 
. Величина этого напряжения равна полуразности наибольшего и наименьшего из главных напряжений
Установим зависимость между относительными деформациями и напряжениями в случае объемного напряженного состояния.
Рассмотрим деформацию элемента, имеющего размеры ребер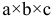 
, по граням которого действуют главные напряжения 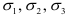(рис. 2.17, а). Для простоты полагаем, что 
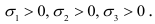. В результате деформации длина ребер элемента изменится и станет равной 
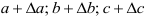(рис. 2.17, б). Относительные удлинения в главных направлениях (т.е. в направлении действия главных напряжений) называют главными удлинениями и соответственно
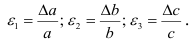
Воспользовавшись принципом независимости действия сил, для главного удлинения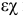 
можно записать следующее равенство:
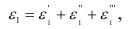
где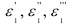 
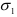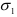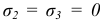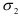— относительные удлинения в направлении вызванные действием соответственно только напряжений (при 
), (при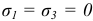 
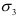) и (при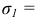 
).
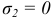В указанном направлении напряжение 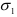вызывает продольную деформацию, а напряжения 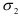и 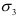— поперечную деформацию Поэтому, используя зависимости (2.1) и (2.3), находим, что
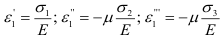
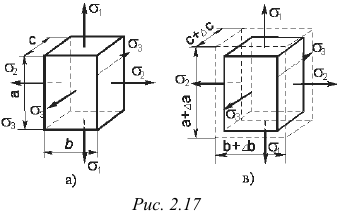
Суммируя относительные удлинения, получим
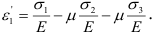
Определяя аналогично главные удлинения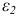 
и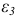 
, окончательно имеем
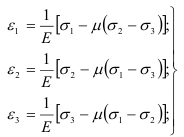
Система равенств (2.25) является математическим выражением обобщенного закона Гука. Полагая в равенствах (2.25) равным нулю одно из главных напряжений, получим закон Гука для плоского напряженного состояния.
Установим связь между главными напряжениями и относительным изменением объема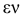 
рассматриваемого элемента. До деформации объема элемента был равен 
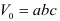, В деформированном состоянии его объем
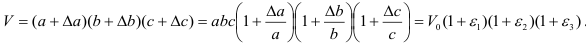
Раскрывая скобки и пренебрегая величинами второго и третьего порядка малости, получим
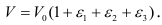
Относительное изменение объема
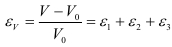
Используя зависимости (2.25), окончательно имеем
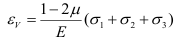
Из формулы (2.26) следует, что для изотропных материалов коэффициент Пуассона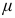 
не может быть больше 0,5. Действительно, например, при растяжении по трем направлениям объем элемента должен увеличиться, т. е. обязательно 
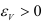. Последнее возможно лишь при условии 
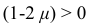, так как
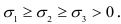
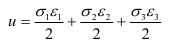
или, используя зависимости (2.25), получим
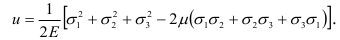
Как уже отмечалось, вследствие упругой деформации в теле накапливается потенциальная энергия деформации. Удельная потенциальная энергия в случае осевого растяжения или сжатия определяется по формуле (2.6). Для объемного напряженного состояния эта энергия, где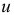 
-полная удельная потенциальная энергия деформации.
Возможны два варианта деформации рассматриваемого элемента. Если все действующие напряжения одинаковы по величине и по знаку (например,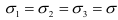 
), то все ребра элемента получат одинаковое изменение длины. Вследствие такой деформации объем элемента изменяется, а его форма остается в первоначальном виде (например, сохраняется форма прямоугольного параллелепипеда). Если же главные напряжения неодинаковы по величине, то вместе с изменением объема элемента произойдет также изменение его формы. Поэтому можно считать, что в общем случае полная удельная потенциальная энергия деформации состоит из двух частей: энергии, накапливаемой за счет изменения объема, и энергии 
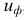накапливаемой вследствие изменения формы:
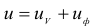
Величина энергии формоизменения
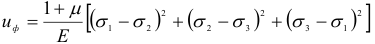
На основании формул (2.27) и (2.28) несложно определить также потенциальную энергию изменения объема.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Допускаемые напряжения и запасы прочности |
| Напряженное состояние при растяжении и сжатии |
| Поперечная сила и изгибающий момент |
| Типы опор и определение опорных реакций. Общие понятия |
