Напряжения и перемещения. Закон Гука
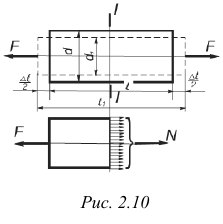
Стержень (рис. 2.10), под действием двух равных по величине и противоположно направленных по его продольной оси сил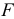 
, претерпевает деформацию растяжения, которая проявляется в изменении длины и поперечных размеров стержня. Его первоначальная длина 
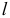увеличивается на величину 
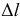, именуемую абсолютным удлинением, и становится равной 
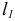Таким образом,
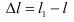
Абсолютное удлинение стержня при данном значении деформирующей силы возрастает с увеличением его первоначальной длины. В связи с этим деформация при растяжении более полно характеризуется относительной величиной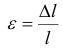 
, которую называют относительным удлинением. Очевидно,
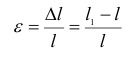
При направлении внешних сил, противоположном указанному на рис. 2.10, стержень испытывает деформацию сжатия. В этом случае называют абсолютным укорочением, так как при сжатии длина стержня уменьшается. Одновременно с продольной деформацией стержень претерпевает поперечную деформацию. При растяжении поперечные размеры уменьшаются, при сжатии — увеличиваются. Относительная поперечная деформация
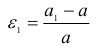
Отношение
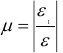
называют коэффициентом Пуассона. Этот коэффициент определяют опытным путем. Для стали
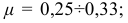
для меди
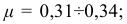
для бронзы
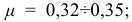
для чугуна
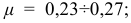
для алюминия
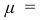
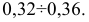
Определим напряжения, возникающие в сечениях стержня, перпендикулярных его оси.
В соответствии с гипотезой плоских сечений полагаем, что для однородного стержня все поперечные сечения при деформации перемещаются параллельно и, следовательно, в них действуют только нормальные напряжения, равномерно распределенные по сечению. Рассечем стержень плоскостью I-I (рис. 2.10, а), перпендикулярной оси стержня. Из условия равновесия части стержня (рис. 2.10, б), принимая во внимание, что равнодействующая внутренних сил упругости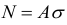 
(где 
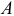— площадь поперечного сечения), имеем 
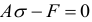. Отсюда напряжение в поперечном сечении стержня при растяжении или сжатии
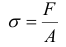
Экспериментальными исследованиями установлено, что в пределах малых удлинений для пластичных материалов имеет место прямая пропорциональная зависимость между напряжениями и деформациями. Эта зависимость носит название закона Гука:
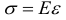
Коэффициент пропорциональности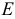 
называется модулем продольной упругости или модулем упругости первого рода, он имеет размерность напряжений 
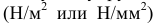и характеризует способность материала сопротивляться упругой деформации при растяжении и сжатии. Величину модуля продольной упругости для различных материалов определяют экспериментально. Для стали
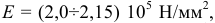
для алюминия
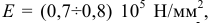
для бронзы
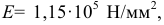
для дерева вдоль волокон
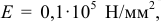
для стеклопластиков
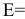
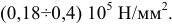
Подставив в формулу (2.3) значение величин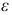 
и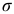 
из формул (2.1) и (2.2), получим
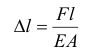
т. е. абсолютное удлинение (укорочение) стержня при растяжении (сжатии) прямо пропорционально растягивающей (сжимающей) силе, длине стержня и обратно пропорционально модулю упругости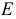 
и площади поперечного сечения 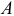. Произведение 
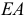называют жесткостью поперечного сечения при растяжении (сжатии).
Область применения закона Гука ограничивается некоторым предельным напряжением, называемым пределом пропорциональности. При напряжении, превышающем предел пропорциональности, линейная зависимость между напряжением и деформацией нарушается.
Величину предела пропорциональности, так же как и других напряжений, характеризующих механические свойства материалов, определяют при испытаниях образцов из различных материалов на растяжение и сжатие.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Понятие о напряжениях |
| Основные гипотезы и допущения |
| Механические характеристики и свойства материалов |
| Допускаемые напряжения и запасы прочности |
