Уравнения движения механизмов с одной степенью свободы. Приведение сил и масс в плоских механизмах
Уравнениями движения механизма называют аналитические зависимости, которые связывают силы, действующие на звенья механизма, с параметрами движения этих звеньев. Уравнения движения записываются с помощью различных принципов и теорем классической механики и могут быть представлены в различных формах. Для записи уравнений движения механизмов с одной степенью свободы чаще используют теорему об изменении кинетической энергии материальной системы.
Согласно теореме об изменении кинетической энергии, перемещение материальной системы из начального положения в конечное равно сумме работ, совершаемых на этом перемещении всеми силами, действующими на систему.
Аналитически теорема (ее интегральная форма) выражается равенством
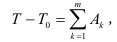
где 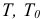 — значения кинетической энергии системы в ее конечном и начальном положениях;
— значения кинетической энергии системы в ее конечном и начальном положениях; 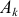 — работа, совершаемая
— работа, совершаемая 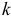 -й из
-й из 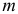 сил, которые действуют на систему при ее перемещении из начального положения в конечное.
сил, которые действуют на систему при ее перемещении из начального положения в конечное.
Кинетическая энергия механизма представляется суммой кинетических энергий подвижных звеньев механизма, имеющих конечную массу:
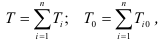
где 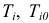 — конечное и начальное значения кинетической энергии
— конечное и начальное значения кинетической энергии 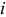 -го звена механизма;
-го звена механизма; 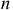 — число подвижных звеньев механизма.
— число подвижных звеньев механизма.
Подставив выражения (1.17) в равенство (1.16), получим уравнение движения механизма в форме интеграла энергии:
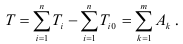
При плоском движении кинетическую энергию любого звена механизма определяют по формуле
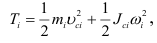
где 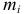 — масса
— масса 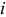 -го звена механизма;
-го звена механизма; 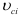 — скорость центра масс
— скорость центра масс 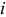 -го звена;
-го звена; 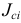 — момент инерции
— момент инерции 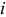 -го звена механизма относительно оси, проходящей через центр масс звена перпендикулярно плоскости движения;
-го звена механизма относительно оси, проходящей через центр масс звена перпендикулярно плоскости движения; 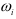 — угловая скорость
— угловая скорость 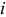 -го звена.
-го звена.
Для 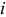 -го звена механизма, которое движется поступательно, полагая в формуле (1.68)
-го звена механизма, которое движется поступательно, полагая в формуле (1.68) 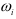 = 0, находим
= 0, находим
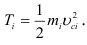
Для 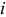 -го звена механизма, которое вращается вокруг неподвижной оси, формула (1.19) вырождается в следующую:
-го звена механизма, которое вращается вокруг неподвижной оси, формула (1.19) вырождается в следующую:
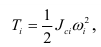
где 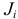 — момент инерции
— момент инерции 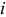 -го звена механизма относительно оси вращения.
-го звена механизма относительно оси вращения.
Уравнение (1.18) даже для плоских механизмов с небольшим числом степеней свободы применяется редко из-за неудобства, связанного с операцией суммирования, которую необходимо выполнять по 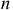 звеньям и
звеньям и 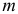 силам. Чаще используют другую формулу уравнения движения, при выводе которой вместо механизма рассматривается его динамическая модель. Уравнение движения механизма заменяется уравнением движения одного его звена (или одной точки звена), называемого звеном (точкой) приведения. За звено приведения обычно выбирают звено, по обобщенной координате которого проводят исследование механизма (начальное звено механизма).
силам. Чаще используют другую формулу уравнения движения, при выводе которой вместо механизма рассматривается его динамическая модель. Уравнение движения механизма заменяется уравнением движения одного его звена (или одной точки звена), называемого звеном (точкой) приведения. За звено приведения обычно выбирают звено, по обобщенной координате которого проводят исследование механизма (начальное звено механизма).
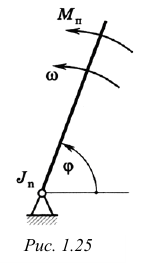
При вращательном движении начального звена механизма уравнение (1.18) заменяется уравнением движения начального звена, принимаемого за звено приведения (рис. 1.25). Момент инерции этого звени 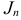 относительно оси вращения называется приведенным моментом инерции. Момент
относительно оси вращения называется приведенным моментом инерции. Момент 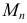 пары сил, действующей на звено приведения, называется приведенным моментом сил.
пары сил, действующей на звено приведения, называется приведенным моментом сил.
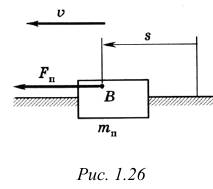
Если начальное звено совершает поступательное движение, то для построения динамической модели механизма выбирается точка 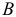 начального звена, принимаемая за точку приведения. В этой точке сосредоточивается приведенная масса
начального звена, принимаемая за точку приведения. В этой точке сосредоточивается приведенная масса 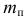 звена. Точка приведения движется под действием приведенной силы
звена. Точка приведения движется под действием приведенной силы 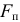 так, что ее обобщенная координата
так, что ее обобщенная координата 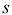 в любой момент времени совпадает с обобщенной координатой механизма (рис. 1.26). Таким образом уравнение движения механизма заменяется уравнением движения одной его точки.
в любой момент времени совпадает с обобщенной координатой механизма (рис. 1.26). Таким образом уравнение движения механизма заменяется уравнением движения одной его точки.
Запишем уравнение движения звена приведения, совершающего вращательное движение, в форме интеграла энергии. Будем считать, что при перемещении звена из начального положения в конечное его обобщенная координата изменяется от 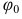 до
до 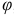 , а приведенный момент инерции — от
, а приведенный момент инерции — от 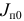 до
до 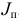 . Тогда уравнение (1.17) переписывается в виде
. Тогда уравнение (1.17) переписывается в виде
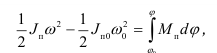
где 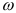 — угловая скорость звена приведения, когда его положение определяется координатой
— угловая скорость звена приведения, когда его положение определяется координатой 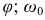 — значение скорости со при
— значение скорости со при 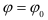 .
.
Необходимые и достаточные условия тождественности уравнений (1.18) и (1.20) выражаются равенствами
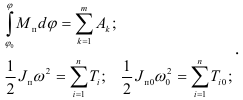
Приведенный момент 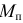 определяется из первого равенства системы (1.70) как момент пары сил, условно приложенной к звену приведения, элементарная работа которой равна сумме элементарных работ сил и пар сил, действующих на звенья механизма. В практических расчетах равенство элементарных работ удобно заменить равенством мощностей:
определяется из первого равенства системы (1.70) как момент пары сил, условно приложенной к звену приведения, элементарная работа которой равна сумме элементарных работ сил и пар сил, действующих на звенья механизма. В практических расчетах равенство элементарных работ удобно заменить равенством мощностей:
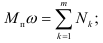
где 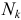 — мощность
— мощность 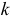 -й силы (момента пары сил), действующей на звено механизма.
-й силы (момента пары сил), действующей на звено механизма.
Если через 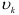 обозначить скорость точки приложения силы
обозначить скорость точки приложения силы 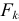 , а через
, а через 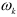 — угловую скорость звена механизма, на которое действует пара сил с моментом
— угловую скорость звена механизма, на которое действует пара сил с моментом 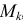 , то соответствующие мощности сил и моментов пар сил определяются формулами
, то соответствующие мощности сил и моментов пар сил определяются формулами
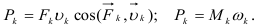
Моменты 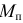 и
и 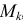 в (1.22) и (1.23) считаются положительными, если их направление совпадает с направлениями угловых скоростей
в (1.22) и (1.23) считаются положительными, если их направление совпадает с направлениями угловых скоростей 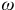 и
и 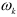 , и отрицательными, если эти направлен: противоположны.
, и отрицательными, если эти направлен: противоположны.
Подставив (1.23) в (1.22), получим формулу для вычислен приведенного момента сил:
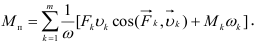
Согласно второму равенству системы (1.21) приведенный момент инерции 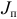 можно определить как момент инерции, которым должно обладать звено приведения относительно оси вращения, чтобы его кинетическая энергия была равна сумме кинетических энергий всех звеньев механизма. Формулу для вычисления приведенного момента инерции можно получить подстановкой (1.19) во второе равенство системы (1.21):
можно определить как момент инерции, которым должно обладать звено приведения относительно оси вращения, чтобы его кинетическая энергия была равна сумме кинетических энергий всех звеньев механизма. Формулу для вычисления приведенного момента инерции можно получить подстановкой (1.19) во второе равенство системы (1.21):
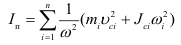
Если начальное звено механизма с одной степенью свободы совершает поступательное движение и приведение осуществляется к некоторой точке звена (точке приведения), то определению подлежат приведенные масса 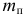 и сила
и сила 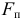 . Приведенной массой механизма та называется такая условная масса, сосредоточенная в точке приведения, при которой кинетическая энергия этой точки равна сумме кинетических энергий всех звеньев механизма. Формула, определяющая приведенную массу
. Приведенной массой механизма та называется такая условная масса, сосредоточенная в точке приведения, при которой кинетическая энергия этой точки равна сумме кинетических энергий всех звеньев механизма. Формула, определяющая приведенную массу 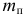 , по аналогии с (1.24) записывается в виде
, по аналогии с (1.24) записывается в виде
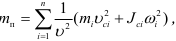
где 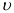 — скорость точки приведения.
— скорость точки приведения.
Приведенной силой 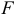 называется условная сила, приложенная в точке приведения, которая определяется из равенства элементарной работы этой силы и суммы элементарных работ сил и пар сил, действующих на звенья механизма. По аналогии с формулой (1.24)
называется условная сила, приложенная в точке приведения, которая определяется из равенства элементарной работы этой силы и суммы элементарных работ сил и пар сил, действующих на звенья механизма. По аналогии с формулой (1.24)
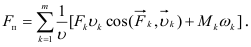
Из формул (1.24) — (1.27) следует, что приведенные сила (момент сил) и масса (момент инерции) зависят не от скорости точки приведения (звена приведения), а от отношения скоростей (аналогов скоростей), которые в свою очередь являются функциями положения звеньев, т. е. функциями обобщенной координаты механизма. Поэтому операция приведения сил и масс механизма может выполняться до решения уравнений движения и определения скоростей точек приведения или угловых скоростей звеньев приведения (и в этом ее важнейшее достоинство). После приведения сил и пар сил, приложенных к звеньям механизма, а также масс и моментов инерции звеньев, динамическая задача о движении механизма как связанной системы звеньев сводится к более простой задаче о движении одного звена (звена приведения) или одной точки этого звена (точки приведения). Уравнение движения механизма в этом случае принимает вид уравнения (1.20), если звено приведения совершает вращательное движение с обобщенной координатой 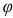 . Если звено приведения движется поступательно с обобщенной координатой
. Если звено приведения движется поступательно с обобщенной координатой 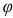 , то уравнение движения механизма переписывается в виде
, то уравнение движения механизма переписывается в виде
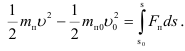
Запись уравнения движения механизма в форме интеграла энергии возможна лишь в ограниченных случаях, например, когда приведенные силы зависят от положений звеньев. При изучении движения механизма в периоды пуска и останова или периодически неравномерного движения используется дифференциальная форма записи уравнений движения, которая получается из дифференциальной формы теоремы об изменении кинетической энергии:
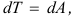
где 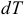 — дифференциал кинетической энергии механизма;
— дифференциал кинетической энергии механизма; 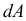 — элементарная работа действующих на механизм сил.
— элементарная работа действующих на механизм сил.
После приведения сил и масс в механизме с вращающимся звеном приведения с помощью (1.29) запишем:
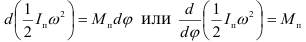
Выполняя дифференцирование в левой части последнего равенства, получим уравнение движения механизма в дифференциальной форме:
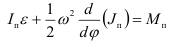
Здесь 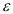 — угловое ускорение звена приведения. Эквивалентная замена
— угловое ускорение звена приведения. Эквивалентная замена 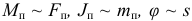 позволяет применить (1.30) для случая, когда звено приведения совершает поступательное движение. Тогда дифференциальное уравнение движения механизма принимает следующий вид:
позволяет применить (1.30) для случая, когда звено приведения совершает поступательное движение. Тогда дифференциальное уравнение движения механизма принимает следующий вид:
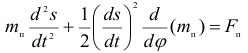
Следует иметь в виду, что уравнения вида (1.30), (1.31) лишь приближенно описывают движение механизма. При определенных условиях (когда, например, приходится учитывать взаимодействие исполнительного механизма с приводным двигателем) они принимают более сложный вид или оказываются связанными с общей системой уравнений, которая описывает работу всего машинного агрегата.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Силы, действующие на звенья механизма, и их классификация |
| Трение в механизмах. Общие сведения о трении в механизмах |
| Коэффициент полезного действия механизма |
| Стадии (режимы) движения механизма |

