Кинематический анализ механизмов графическим методом

Кинематический анализ механизмов графическим методом

Решение задач о положениях, скоростях и ускорениях графическим методом поясним на примере кинематического анализа механизма плоского шарнирного четырехзвенника (рис. 1.19, а). Механизм имеет одну степень подвижности и состоит из ведущего звена 1 (кривошипа) и стойки 4, к которым присоединена одна группа Ассура 2-го класса, составленная из звеньев 2 (шатуна) и 3 (коромысла). За обобщенную координату принят угол поворота .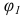

Определение положений (траекторий точек звеньев). Решить задачу о положениях (построить план положений) значит графически изобразить кинематическую схему механизма для заданного значения координаты 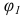. Для построения схемы механизма выберем масштаб построений (м/мм):

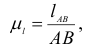
где 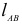— длина звена 1, м; 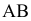— отрезок, изображающий звено 1 на чертеже, мм. Величины 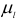, целесообразно принимать по стандарту ЕСКД для выполнения чертежей деталей узлов машин.

Длины отрезков на чертеже, изображающих звенья механизма, представим в виде

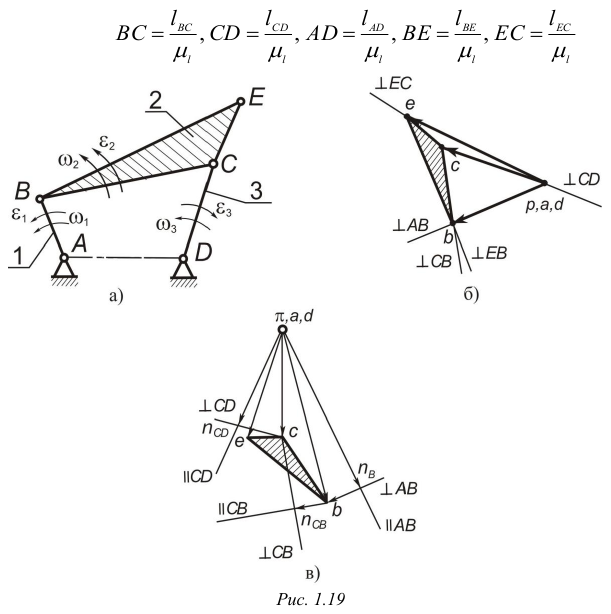
Вычислив длины отрезков, простым геометрическим построением получим план положения механизма для данного значения угла 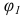(рис. 1.19, а). Построив планы положений механизма для 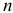-го количества значений угла 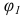получим траектории движения точек звеньев механизма.

ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ

(рис. 1.19, б). Данную задачу решают методом построения плана скоростей. Планом скоростей (ускорений) называется фигура, составленная из векторов абсолютных скоростей (ускорений) точек звеньев, выходящих из одной точки 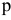( 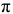для плана ускорений), называемой полюсом плана скоростей (ускорений), и векторов относительным скоростей (ускорений), соединяющих концы векторов абсолютных скоростей (ускорений).

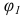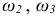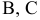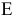Сначала для заданного положения механизма (задано значение угла ) с известными размерами его звеньев строится план положений. При заданной угловой скорости ведущего звена со, требуется определить угловые скорости звеньев 2, 3, а также скорости характерных точек и звеньев механизма (см. рис. 1.19, а).

Скорость точки 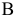ведущего звена 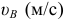и масштабный коэффициент 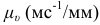определяются выражениями:

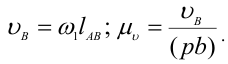
Здесь 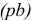— длина отрезка, изображающего скорость 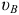на плане скоростей (выбирается максимально возможным для имеющегося места построения плана скоростей (ускорений) и таким, чтобы масштабный коэффициент 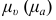выражался одной цифрой (см. масштабы ЕСКД для чертежей деталей и сборочных единиц) или двумя цифрами.

Для построения плана скоростей составляется два векторных уравнения скоростей на каждую группу Ассура 2-го класса, начиная с первой группы, присоединенной к ведущему звену. Скорости точек, принадлежащих внешним кинематическим парам группы, известны:

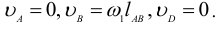
Искомой является скорость точки 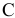, которая принадлежит внутренней кинематической паре группы и, следовательно, звеньям 2 и 3 одновременно.

Первое векторное уравнение скоростей запишем, рассмотрев движение звена 2. Шатун 2 совершает плоскопараллельное движение, поэтому абсолютную скорость точки 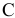можно предоставить суммой скоростей переносного и относительного движений. Переносным движением является поступательное движение звена 2 со скоростью точки 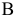, а относительным — вращательное движение этого звена вокруг точки 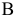. Используя теорему сложения скоростей, имеем

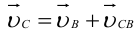
где 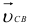— вектор скорости точки 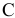во вращательном движении звена 2 относительно точки .

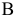По аналогии составим второе векторное уравнение скоростей движения звена 3:

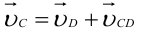
где 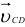— вектор скорости точки 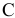во вращательном движении звена 3 относительно неподвижной точки .

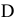Решая графически уравнения (1.5) и (1.6) находим абсолютную 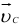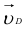и относительную 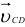скорости токи 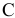. Результат графического решения этих уравнений векторные треугольники скоростей — план скоростей.

Построение плана скоростей начинаем с выбора полюса: на плоскости чертежа отмечаем произвольную точку 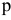(рис. 1.19, б). Из полюса 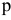откладываем отрезок 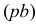. Рекомендуемой выше длины, направленный перпендикулярно звену 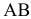в сторону, соответствующую направлению вращения звена 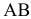. Затем из точки 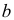проводим линию действия вектора 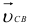, перпендикулярную звену 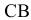, и выполняем построение векторного треугольника, соответствующего уравнению (1.6). Так как 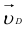= 0, конец вектора 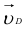(точка 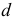на плане скоростей) совпадает с полюсом 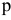. Из точки 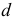проводим линию действия вектора 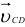, направленную перпендикулярно звену 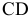. Пересечение построенных линий (точка 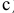) определяет положение конца векторе скорости 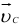. Вектор скорости 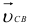изображается на плане скоростей отрезком .

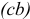При определении направлений векторов на плане скоростей руководствуемся следующими правилами. Вектор абсолютной скорости всегда направлен из полюса; вектор относительной скорости — к точке плана, соответствующей первой букве индекса в обозначении этой скорости. Таким образом, стрелку вектора 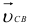на плане скоростей направляем из точки 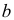в точку 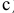. Вектор 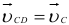, изображаемый отрезком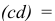 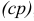также направлен в точку с плана.

Учитывая, что точк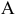а звена 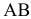неподвижна, соответствующую точку 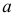на плане совмещаем с полюсом 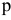. На этом заканчивается построение плана скоростей механизма. Значения искомых скоросте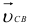й и 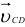находятся путем замера длин отрезков 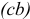и :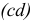

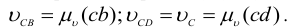
При определении угловых скоростей звеньев механизма используем полученные выше результаты. Модуль угловой скорости вращения шатуна (звена 2) подсчитываем по формуле

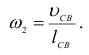
Для определения направления вращения шатуна со скоростью 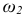перенесем вектор 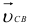параллельно самому себе из плана скоростей в точку 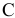механизма. Направление вектора 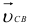в показывает, что вращение шатуна будет направлено против хода часовой стрелки.

Аналогичные операции проводим при определении угловой скорости вращения звена 3:

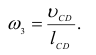
Параллельный перенос вектора 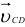в точку 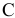механизма позволяет установить, что вращение звена 3 с угловой скоростью 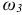направлено, как и вращение шатуна 2, против хода часовой стрелки. На схеме механизма, изображенной на рис. 1.19, а, направления вращения звеньев указаны круговыми стрелками.

После построения плана скоростей и определения угловых скоростей звеньев механизма появляется возможность определения скорости любой точки механизма. Допустим, требуется найти скорость точки 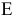шатуна 2 (рис. 1.19, а). Составляем два векторных уравнения, аналогичных уравнениям (1.5) и (1.6):

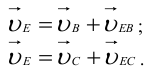
Направление векторов 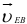и :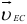

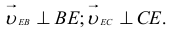
Теперь можно определить абсолютную скорость 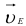, достроив план скоростей. Из точки 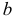плана проводим линию, перпендикулярную 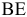, а из точки 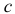— линию, перпендикулярную 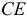. Точка 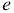пересечений этих линий определяет положение конца вектора 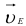. Соединив точку 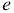с полюсом 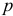, получим отрезок 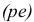, с помощью которого вычисляем значение скорости

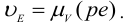
Обратим внимание на следующее свойство плана скоростей. Стороны 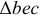плана скоростей и 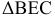плана положений механизма взаимно перпендикулярны и, следовательно, эти треугольники подобны. Вершины треугольников сходственно расположены, т.е. обход контуров 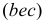и 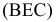происходит в одном направлении, в данном случае по ходу часовой стрелки. Это свойство справедливо как для плана скоростей, так и для плана ускорений любых точек одного и того же звена механизма. Оно формулируется в виде теоремы подобия: отрезки прямых, соединяющих концы векторов абсолютных скоростей (или ускорений) точек одного и того же звена на плане скоростей (или ускорений), и отрезки прямых, соединяющих соответствующие точки самого звена на плане положений механизма, образуют подобные и сходственно расположенные фигуры.

С помощью этой теоремы можно найти скорость (или ускорение) любой точки звена путем построения подобных и сходственно расположенных фигур по известным скоростям двух точек этого звена.

ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ

(рис. 1.19, в). Для определения ускорений точек звеньев механизма построим план ускорений. Построения проведем на примере того же шарнирного четырехзвенника при заданном значении обобщенной координаты 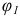Считаются известными угловая скорость 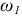и угловое ускорение 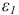ведущего звена.

Как известно, ускорение любой точки звена, которое совершает вращательное движение вокруг неподвижной оси, можно представить суммой:

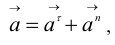
где 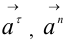— соответственно касательная (тангенциальная) и нормальная составляющие ускорения .

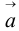Ведущее звено (кривошип) четырехзвенника вращается вокруг точки 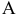. Поэтому ускорение точки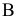

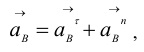
где

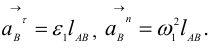
Нормальная составляющая 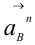ускорения точки 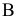направлена к центру вращения (к точке 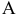) параллельно 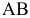. Касательная, составляющая 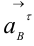направлена перпендикулярно 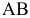в сторону, совпадающую с направлением ускорения .

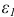На плане ускорений конец вектора нормальной составляющей ускорения точки обозначим буквой с соответствующим точке индексом:

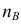— конец вектора 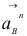на плане ускорений; 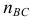— конец вектора .

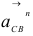Зададимся отрезком 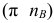, изображающим нормальную составляющую ускорения точки 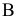, и определим масштабный коэффициент плана ускорений (в 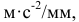смотри рекомендации по величинам отрезков на плане скоростей (ускорений) на с. 20).

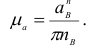
По аналогии с задачей о скоростях составим два векторных уравнения для ускорения точки 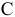, принадлежащей звеньям 2 и 3:

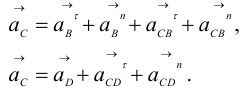
В (1.11) 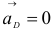, а ускорения 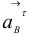и 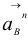уже определены по величине и направлению. Значения 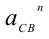и 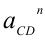вычисляем по формулам

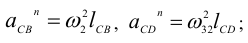
отрезки, которые изображают эти ускорения на плане ускорений (рис. 1.19, в) — по формулам

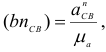
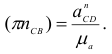
Построение плана ускорений продолжаем непосредственно по уравнениям (1.11). От произвольной точки я (полюса) откладываем отрезок 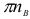параллельно 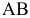в направлении от 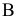к 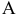. Из точки 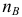проводим отрезок 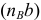, изображающий ускорение 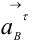Соединив точку 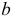с полюсом 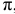, получим отрезок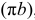, изображающий ускорение 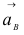. Стрелки, указывающие направление полученных векторов, расставляются согласно правилу векторного суммирования.

Для завершения графического решения уравнений (1.11) из точки 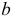откладываем отрезок 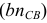параллельно шатуну 2 в направлении от точки 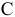к точке 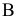, а из точки 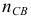перпендикулярно шатуну проводим линию действия вектора ускорения .

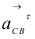При построении плана ускорений, учтем, что ускорение точки 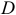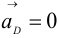и следовательно точка 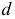плана ускорений совпадает с полюсом 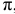. Из точки 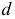нанесем параллельно 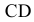отрезок 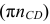, изображающий вектор нормального (центростремительного) ускорения точки 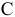относительно точки 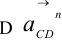, направленного к точке 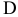. Из точки 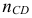перпендикулярно 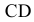проведем линию действия вектора тангенциального (касательного) ускорения 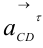. Пересечение линий действия ускорени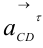й и 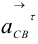определяет точку 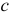— конец вектора искомого ускорения 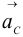. Соединив точку 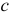и полюс 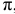и замерив длину отрезка 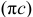, получим общее ускорение точки 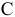. Закончив построение плана ускорений, находим неизвестные ускорения

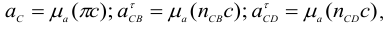
а затем угловые ускорения звеньев:

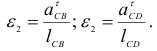
Направления ускорени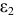й и 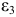, условно показанные на рис. 1.19, а, круговыми стрелками, определяют векторы 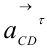и 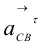, перенесенные с плана ускорений в точку 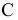механизма.

Для нахождения ускорения 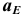точки 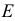шатуна используем свойство подобия плана ускорений. На отрезке 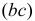плана ускорений строим 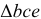, подобней 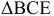плана положений и сходственно с ним расположенный (порядок расположения букв на плане ускорений и на механизме на любом направлении их прочтения. Полученную точку 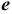соединим с полюсом .

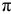Тогда 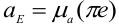. Аналогичными построениями определяется ускорение любой другой точки механизма. Таким образом, на основании изложенного выше видим, что планы скоростей (ускорений) — это результат решения графическим путем векторных уравнений, определяющих скорости (ускорения) соответствующих точек звеньев механизмов.

Эта теория взята со страницы лекций по предмету «прикладная механика»:

Предмет прикладная механика

Возможно эти страницы вам будут полезны:

Структурно-конструктивная функциональная классификация механизмов

Задачи и методы кинематического анализа

Цели и задачи динамического анализа

Силы, действующие на звенья механизма, и их классификация