Степень подвижности кинематической цепи
Число возможных независимых движений кинематической цепи относительно одного из звеньев называют степенью ее подвижности. Для определения степени подвижности кинематической цепи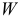 
необходимо из общего числа степеней подвижности всех ее подвижных звеньев вычесть число связей, накладываемых на относительное движение звеньев кинематическими парами, которыми соединены звенья. Пусть 
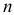— число подвижных звеньев пространственной кинематической цепи; 
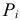— число кинематических пар 
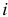-го класса 
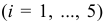. Тогда 6 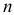— общее число степеней подвижности 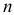звеньев цепи, считая их не связанными между собой, a 
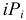— общее число связей, наложенных на звенья механизма кинематическими парами 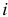-го класса.
С помощью введенных обозначений степень подвижности кинематической цепи можно определить по выражению
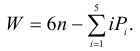
Развернув сумму в выражении (1.1), получим структурную формулу (математическую модель)пространственной кинематической цепи общего вида (формулу Сомова-Малышева):
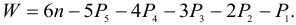
Формула (1.2) показывает, какому количеству звеньев кинематической цепи должно быть задано движение (т. е. сколько должно быть ведущих звеньев), чтобы движение остальных звеньев было определенным, единственно возможным. Формулой можно пользоваться, если учесть дополнительные общие условия связи, которые накладывают ограничения на движение всех звеньев кинематической цепи. Например, для плоской кинематической цепи, у которой звенья движутся параллельно одной неподвижной плоскости, перпендикулярной осям вращательных пар, на них наложены три общие связи (см. рис. 1.1). Звенья такой цепи не могут перемещаться вдоль оси, перпендикулярной к неподвижной плоскости, и вращаться относительно двух осей, лежащих в этой плоскости. Число степеней подвижности каждого звена дополнительно уменьшается здесь на 3 — число общих связей. Общее число степеней подвижности 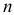звеньев цепи будет равно (6-3)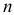, т.е. каждая кинематическая пара в этом случае накладывает на движение звеньев цепи на три ограничения меньше класса пары. Так, пары 5-го и 4-го классов (только они могут быть использованы в этом случае) накладывают на движение звеньев плоской кинематической цепи соответственно две и одну связи, а кинематические пары 1-го, 2-го и 3-го классов в такой (плоской) кинематической цепи не могут быть использованы.
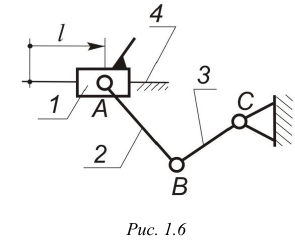
Для плоской кинематической цепи структурная формула (1.2) имеет вид (формула Чебышева)
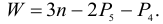
Кинематические пары 5-го класса в плоском механизме могут существовать в виде вращательной и поступательной пар (см. табл. 1.1).
Поскольку механизм представляет собой кинематическую цепь, то степень его подвижности определяется по формулам (1.2), (1.3) с учетом общих связей, наложенных на все звенья механизма. Степень подвижности механизма соответствует количеству независимых (обобщенных координат), которое необходимо задать для однозначной определенности положений всех звеньев механизма. Так, для механизма шарнирного четырехзвенника имеем (см. рис. 1.1).
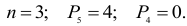
Степень подвижности подсчитываем по формуле (1.3):
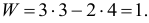
Следовательно, данный механизм должен иметь одно ведущее звено и одну обобщенную координату. В качестве обобщенной координаты обычно выбирают угловую координату ведущего звена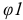 
.
Для кривошипно-ползунного механизма (рис. 1.6) параметры формулы (1.3) такие же, как и для механизма шарнирного четырехзвенника. Ведущее звено (ползун 1) движется прямолинейно, и за обобщенною координату принимается линейная координата ползуна.
В механизмах с двумя степенями подвижности за обобщенные координаты выбираются координаты двух ведущих звеньев или одного ведущего звена, если это звено образует со стойкой кинематическою пару с двумя степенями свободы подвижности
Структурные формулы механизмов (1.2) и (1.3), полученные с применением понятия «класс кинематической пары» на наш взгляд проще и понятнее можно получить используя понятие «степеней подвижности кинематической пары» — число возможных независимых движений одного звена относительно другого, которые позволяет совершать данная кинематическая пара. С этих позиций все кинематические пары (табл. 1.1) можно поделить пары от пятиподвижной (шар на плоскости) до од-ноподвижной (только с вращательным или только с поступательным движением).
Если обозначить, как и выше,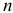 
— число подвижных звеньев кинематической цепи (механизма), 
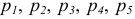— числа соответственно одно-, двух-, трех-, четырех- и пятиподвижных кинематических пар, то структурная формула пространственного механизма с учетом приведенных выше пояснений будет иметь вид,
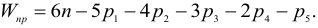
Для плоского механизма
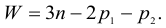
Формулы (1.2), (1.3), (1.2′), (1.3′) справедливы для механизмов без избыточных (пассивных) связей и лишних степеней подвижности. Однако часто для выполнения специальных требований в механизм включают дополнительные элементы и звенья, которые не оказывают влияния на движение остальных звеньев и называются пассивными. Избыточными (пассивными) связями в механизме называют повторяющиеся связи, которые дублируют ограничения, наложенные другими связями. Избыточные связи можно устранить из механизма, сохранив при этом задание точных условий связи. Для изучения движения механизмов их следует удалить и учитывать только те связи и степени подвижности, от которых зависит определенность их движения.
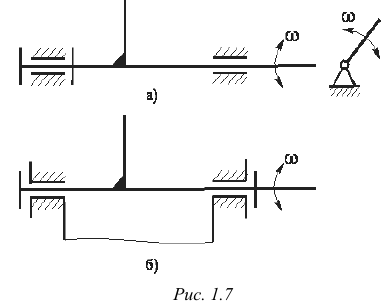
Так, например, простейший двухзвенный механизм, состоящий из стойки и вращающегося звена — ротора (электродвигатели, электрогенераторы, турбины различных типов и т.д.) имеют две опоры, а не одну, как это необходимо с точки зрения кинематики такого устройства (рис. 1.7 а). Степень подвижности такого механизма по зависимости (1.3′) обусловлена введением дополнительной (правой) опоры, создавшей избыточную (пассивную связь). В действительности при надлежащей точности изготовления опор левой и правой (расточка отверстий и окончательная обработка опорных мест вала за одну установку) действительная степень подвижности и теоретическая равны единице (рис. 1.7 б).
Избыточную (пассивную) подвижность, не влияющую на движение ведомого звена, можно обнаружить у механизма пространственного четырехзвенника, рис. 1.4, для которого степень подвижности по выражению (1.2′)
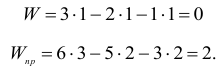
У этого механизма избыточная подвижность обусловлена возможностью вращения звена 2 относительно его продольной оси.
Избыточная подвижность имеется у кулачковых механизмов, у которых толкатель снабжен роликом, вращательное движение которого не влияет на движение этого толкателя.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Классификация кинематических пар |
| Кинематические цепи |
| Структурно-конструктивная функциональная классификация механизмов |
| Принципы строения и структурная классификация механизмов |
