Оглавление:
Кредитные операции
Кредитные операции играют основную роль в деятельности банков. Ставка, по которой выдаются кредиты, превышает ставку, по которой принимаются депозиты, на величину процентной маржи, которая и является источником прибыли банка от кредитных операций. При погашении кредита удобно сразу определять размер возвращаемой (погашаемой) суммы, равной сумме кредита 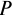 с начисленными процентами
с начисленными процентами 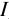 , которая при использовании простой ставки процентов определяется так:
, которая при использовании простой ставки процентов определяется так:
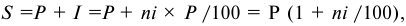
где 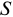 — наращенная сумма платежа по начисленным процентам;
— наращенная сумма платежа по начисленным процентам; 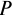 — сумма первоначального долга;
— сумма первоначального долга; 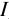 — сумма процентов;
— сумма процентов; 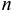 — число полных лет;
— число полных лет; 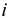 — ставка процентов (в долях единиц).
— ставка процентов (в долях единиц).
Если ставка процентов в течение срока кредита по условиям кредитного договора будет изменяться, размер погашаемой суммы можно определить, применяя формулу 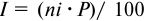 для интервалов, на которых ставка процентов будет постоянной. При
для интервалов, на которых ставка процентов будет постоянной. При 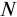 интервалах начисления процентов, на каждом из которых будет применяться своя годовая простая ставка процентов
интервалах начисления процентов, на каждом из которых будет применяться своя годовая простая ставка процентов 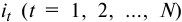 , сумму процентов составит можно определить так:
, сумму процентов составит можно определить так:
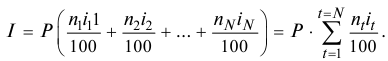
Сумма кредита с процентами определяется по формуле
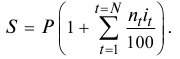
При выдаче кредитов на срок больше года проценты могут начисляться по сложной годовой ставке. Погашаемая сумма кредита может быть при этом определена с использованием формулы
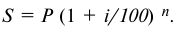
При начислении процентов за кредит следует учитывать инфляцию. Ставку процентов при выдаче кредитов в условиях инфляции можно определить следующим образом. Если задана реальная доходность кредитной операции, определяемая простой ставкой процентов 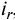 , то для суммы кредита
, то для суммы кредита 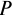 погашаемая сумма при отсутствии инфляции определялась бы по формуле
погашаемая сумма при отсутствии инфляции определялась бы по формуле
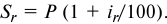
Эквивалент такой суммы в условиях инфляции составит:
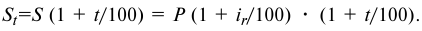
С другой стороны, величину 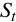 можно записать в виде
можно записать в виде
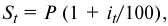
где 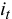 — простая ставка процентов за срок кредита, учитывающая инфляцию.
— простая ставка процентов за срок кредита, учитывающая инфляцию.
Приравняв два последних выражения, получаем
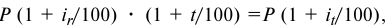
откуда простая ставка процентов, обеспечивающая реальную эффективность кредитной операции 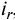 при уровне инфляции за срок кредита
при уровне инфляции за срок кредита 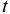 , будет определяться по формуле
, будет определяться по формуле
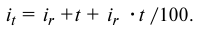
При проведении подобных расчетов часто пользуются приближенным выражением
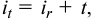
из которого следует, что
Следовательно, если кредит был выдан по ставке 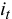 , которая меньше уровня инфляции, или уровень инфляции за срок кредита оказался выше расчетного, реальная эффективность кредитной операции с учетом инфляции будет отрицательной (банк реально понесет убытки).
, которая меньше уровня инфляции, или уровень инфляции за срок кредита оказался выше расчетного, реальная эффективность кредитной операции с учетом инфляции будет отрицательной (банк реально понесет убытки).
Если срок, на который выдается кредит, меньше срока, за который определяется расчетный уровень инфляции, необходимо задать зависимость значения 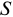 от срока кредита, т.е. ответить на вопрос: если, например, за год цены вырастут на столько-то процентов, на сколько процентов они вырастут за заданную часть года? Самым простым способом является задание линейной (пропорциональной) зависимости вида
от срока кредита, т.е. ответить на вопрос: если, например, за год цены вырастут на столько-то процентов, на сколько процентов они вырастут за заданную часть года? Самым простым способом является задание линейной (пропорциональной) зависимости вида
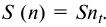
При заданном годовом уровне инфляции 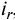 мы, используя приведенную выше методику, для ставки процентов при выдаче кредита на срок меньше года, получаем:
мы, используя приведенную выше методику, для ставки процентов при выдаче кредита на срок меньше года, получаем:
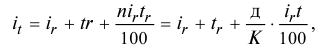
где 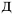 — срок кредита в днях;
— срок кредита в днях; 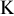 — количество дней в году.При выдаче долгосрочных кредитов сложную ставку процентов
— количество дней в году.При выдаче долгосрочных кредитов сложную ставку процентов 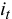 обеспечивающую при годовом уровне инфляции
обеспечивающую при годовом уровне инфляции 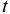 реальную эффективность кредитной операции
реальную эффективность кредитной операции 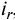 и определяемую аналогичным образом, можно вычислить по формуле:
и определяемую аналогичным образом, можно вычислить по формуле:
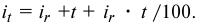
Задача 71.
Банк выдал кредит в размере 500 тыс. руб. на шесть месяцев по простой ставке процентов 18% годовых. Требуется определить:
1) погашаемую сумму.
2) сумму процентов за кредит.
Решение:
- Погашаемую сумму определим по формуле (5.1):

- Сумма процентов, полученная банком за кредит, будет равна:
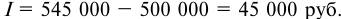
Задача 72.
Банк выдал кредит в сумме 500 тыс. руб. на три квартала по простой ставке процентов, которая в первом квартале составила 15% годовых, а в каждом последующем увеличивалась на 1 процентный пункт. Требуется определить:
1) погашаемую сумму;
2) сумму процентов за пользование кредитом.
Решение:
1. По формуле (5.2) определяем погашаемую сумму:
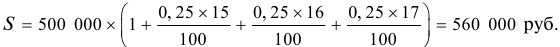
- Сумму полученных процентов вычисляем так:
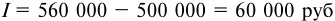
Задача 73.
Банк выдал долгосрочный кредит в размере 5 млн. руб. на пять лет по годовой ставке сложных процентов 20% годовых. Кредит должен быть погашен единовременным платежом с процентами в конце срока. Требуется определить:
1) погашаемую сумму
2) сумму полученных процентов.
Решение:
- По формуле
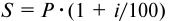
определяем погашаемую сумму:
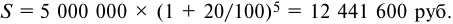
- Сумму полученных процентов вычисляем так:
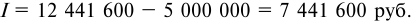
Задача 74.
Банк выдал кредит в 1 млн руб. на год. Требуемая реальная доходность операции равна 8% годовых, ожидаемый годовой уровень инфляции принят равным 60%. Требуется определить:
1) ставку процентов по кредиту.
2) погашаемую сумму и сумму полученных процентов.
Решение:
- По формуле (5.4) вычислим ставку процентов по кредиту:
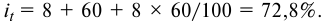
- По формуле (5.3) определим погашаемую сумму:
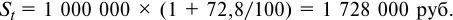
Сумму полученных процентов определяем так:
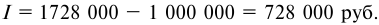
Задача 75.
Кредит в 500 тыс. руб. выдан на 200 дней. Расчетный уровень инфляции за год принят равным 80%, реальная доходность операции должна составить 12% годовых, количество дней в году равно 365. Требуется определить:
1) ставку процентов при выдаче кредита
2) погашаемую сумму и сумму полученных процентов.
Решение:
- По формуле (5.5) определим ставку процентов:
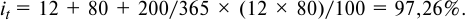
- По формуле (5.1) определим погашаемую сумму:
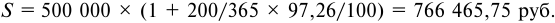
Сумма полученных процентов составит:
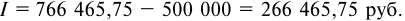
Задача 76.
Кредит в 2 млн руб. выдан на два года. Реальная эффективность операции должна составить 8% годовых по сложной ставке процентов. Расчетный уровень инфляции 20% в год. Требуется определить:
1) ставку процентов при выдаче кредита;
2) погашаемую сумму и сумму полученных процентов. Решение
- По формуле (5.6) определяем ставку сложных процентов:
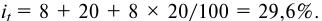
- По формуле
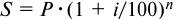
определим погашаемую сумму:
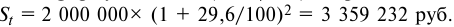
Сумма полученных процентов будет равна:
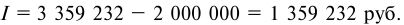
Задача 77.
Базовая годовая сумма оплаты обучения в вузе равна 2000 руб. и повышается с учетом инфляции (10%). Срок обучения пять лет. Вуз предлагает выплатить сразу 10 тыс. руб., оплатив весь срок обучения. Банковский процент на вклад составляет 12%, сумма вклада равна 12 тыс. руб. Требуется определить, выгодно ли это предложение для студента.
Решение:
Проведем расчеты в табл. 5.6 и 5.7.
- Определим потоки средств при ежегодной оплате.
- Определим потоки средств при разовом взносе.
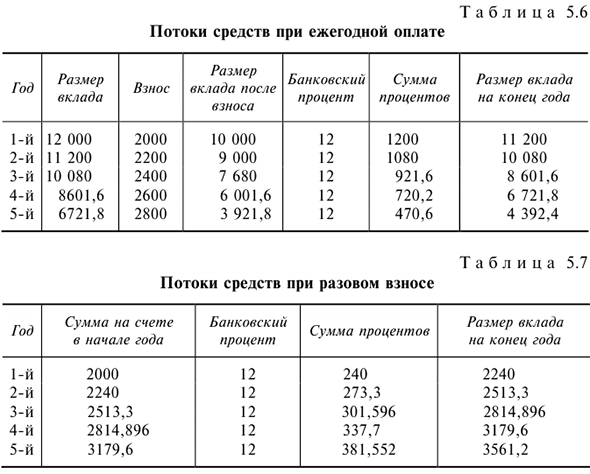
По результатам расчетов видно, что первый вариант выгоднее.
Задача 78.
В расчет за поставку фирма  получила от своего клиента переводной вексель на сумму 100 тыс. руб. с датой истечения срока действия через 30 дней. Фирма
получила от своего клиента переводной вексель на сумму 100 тыс. руб. с датой истечения срока действия через 30 дней. Фирма  дисконтирует вексель в своем банке, который применяет учетную ставку 4%. Требуется определить:
дисконтирует вексель в своем банке, который применяет учетную ставку 4%. Требуется определить:
1) сумму дисконта;
2) сумму, которую банк выплачивает фирме 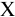 .
.
Решение:
Используем формулу расчета дисконта:

- Определяем сумму дисконта:
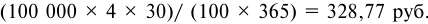
- Определяем выплачиваемую сумму:
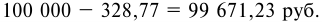
Задача 79.
Заемщик берет ссуду на сумму 100 тыс. руб. сроком на шесть месяцев. Через шесть месяцев заемщик возмещает 102 тыс. руб., т.е. ссуду — 100 тыс. руб. и проценты — 2 тыс. руб. Требуется определить годовую ставку по ссуде.
Решение:

Задача 80.
Банк выдал в начале квартала кредит на сумму 100 млн руб. сроком на один месяц по ставке 20% годовых и через месяц кредит на сумму 200 млн руб. сроком на два месяца по ставке 25% годовых. Требуется определить сумму процентов за кредиты (полученный доход).
Решение:
Используем формулу
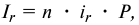
где 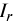 — сумма процентов за год;
— сумма процентов за год; 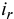 — годовая ставка процентов;
— годовая ставка процентов; 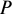 — сумма, на которую начисляются проценты;
— сумма, на которую начисляются проценты; 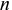 — число лет.
— число лет.
- Сумма процентов за первый кредит:
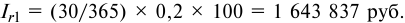
- Сумма процентов за второй кредит:

- Общий процентный доход:
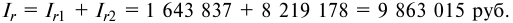
Задача 81.
Банк выдал ссуду в размере 1 млн руб. на шесть месяцев по простой ставке процентов 16% годовых. Требуется определить: сумму погашения.
Решение:
Используем формулу:
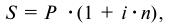
где 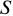 — наращенная сумма платежа;
— наращенная сумма платежа; 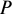 — сумма выданной ссуды;
— сумма выданной ссуды; 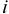 — ставка процентов;
— ставка процентов; 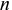 — период погашения;
— период погашения; 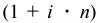 — множитель наращивания.
— множитель наращивания.
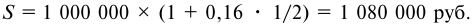
Задача 82.
При выдаче кредита на шесть месяцев по ставке 16% годовых удержаны комиссионные в размере 2% суммы кредита. Требуется определить доход банка с учетом удержания комиссионных.
Решение:
Используем следующую формулу:
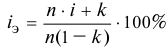
где 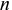 — срок кредита в годах;
— срок кредита в годах; 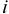 — ставка кредита;
— ставка кредита; 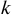 — ставка комиссионных.
— ставка комиссионных.
Доход банка составит в данном случае:
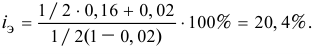
Эта лекция с примерами решения взята со страницы решение задач по предмету «деньги кредит банки»:
Деньги кредит банки задачи с решениями
Возможно эти страницы вам будут полезны:

