Оглавление:
Обоснование метода.
Метод узловых потенциалов обоснован на составлении уравнений по первому закону Кирхгофа и закону Ома для участка цепи, содержащего ЭДС. Число уравнений в стандартной системе на единицу меньше общего числа узлов, то есть к-1, поэтому целесообразно на первом этапе выполнить упрощение схемы с уменьшением числа узлов.
Так в схеме рисунка 3.52 проставим положительные направления токов и объединяем узлы 1 и 8, 3 и 9, 4 и 5, 2 и 10, а трёхлучевую «звезду» сопротивлений 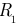 и преобразуем в треугольник сопротивлений величиной 3
и преобразуем в треугольник сопротивлений величиной 3 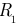 .
.
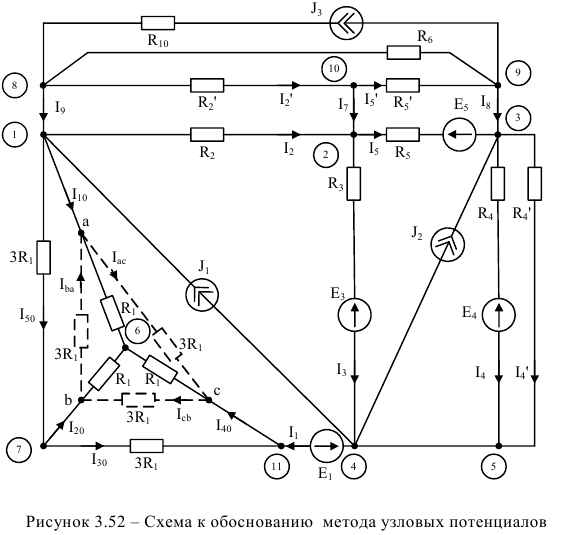
В упрощённой схеме рисунка 3.53 четыре узла и десять неизвестных токов. Три уравнения составим для узлов 1,2 и 3 по первому закону Кирхгофа для узлов (1 ),(2) и (3), а остальные семь по закону Ома для ветви содержащей ЭДС (рисунок 3.53):
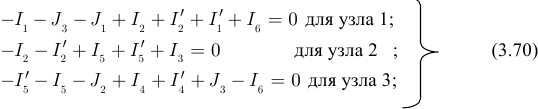
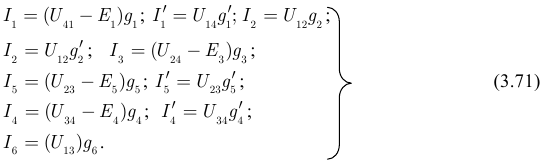
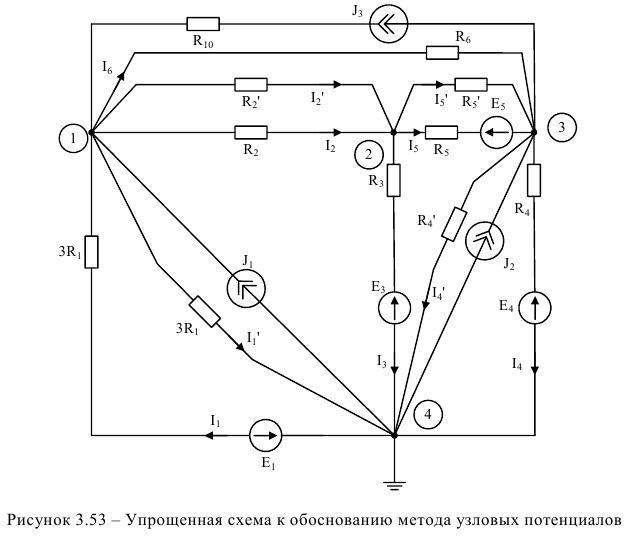
Здесь:
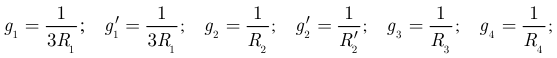
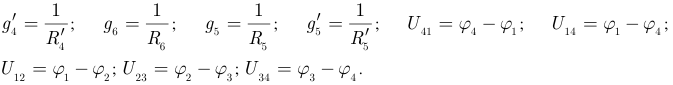
Решаем систему уравнений подстановкой величин токов (3.71) в уравнения (3.70) получим:
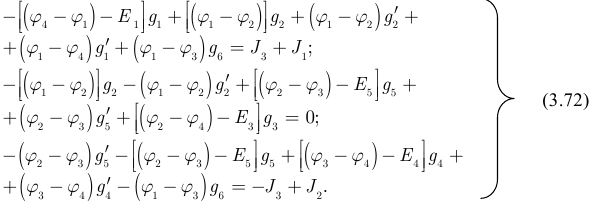
Если принять потенциал самого старшего по номеру узла 4 равным нулю («заземлить»), и сгруппировать коэффициенты при одинаковых потенциалах получим систему уравнений:
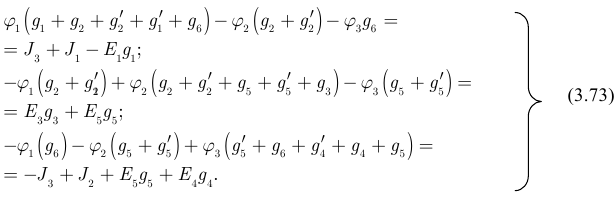
Полученная система уравнений (3.73) содержит ряд особенностей:
- В левой части каждого из уравнений потенциал, для каждого составленного уравнения умножается на сумму проводимостей ветвей, подсоединенных к данному узлу.
Такие суммы называют собственными проводимостями узлов и их обозначают:
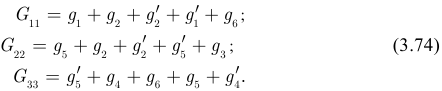
- Узловые потенциалы, номера которых не совпадают с номером узла, для которого составлено данное уравнение, умножается на взятые со знаком минус проводимости ветвей, подсоединеных между этим и другими узлами.
Такие суммы называют взаимными проводимостями ветвей и для них вводят обозначения:
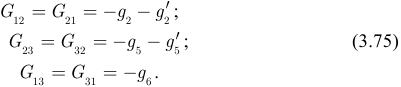
Правая часть каждого из уравнений системы является алгебраической суммой токов, источников тока и произведений ЭДС ветвей на собственные проводимости ветвей, подсоединенных к узлу, для которого составлено уравнение; токи и ЭДС источников, направленных к узлу, имеют знак плюс, а если от узла — знак минус. Такие алгебраические суммы называют узловыми токами и вводят обозначения:
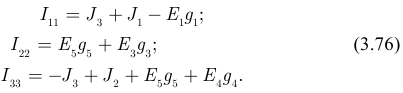
С учетом введенных обозначений система уравнений (3.73) принимает вид:
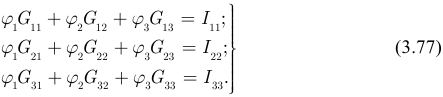
Полученная система уравнений (3.77) является стандартной формой записи уравнений в методе узловых потенциалов, и для случая цепи с 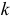 узлами система имеет вид:
узлами система имеет вид:
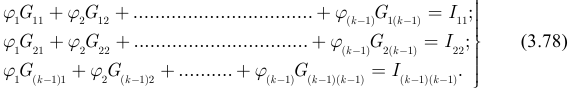
В матричной форме:

где: 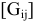 — квадратичная матрица собственных и взаимных проводимостей узлов или матрица проводимостей;
— квадратичная матрица собственных и взаимных проводимостей узлов или матрица проводимостей; 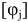 — матрица-столбец узловых потенциалов;
— матрица-столбец узловых потенциалов; 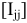 — матрица-столбец узловых токов источников тока и ЭДС;
— матрица-столбец узловых токов источников тока и ЭДС; 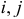 — номера рядка и столбца элементов матриц.
— номера рядка и столбца элементов матриц.
Матрица проводимостей симметричная, так как:
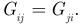
Решение системы (3.78) относительно матрицы узловых потенциалов имеет вид:

где: 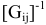 — обратная матрица проводимостей.
— обратная матрица проводимостей.
Решение системы уравнений (3.78) с применением определителей имеет вид:
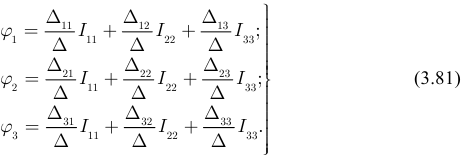
где: 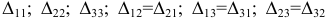 — алгебраические дополнения, а
— алгебраические дополнения, а  — главный определитель системы уравнений.
— главный определитель системы уравнений.
Вычисление определителей выполняют по формулам таким же, как и в методе контурных токов (3.59). По формулам (3.71) рассчитываем величины токов в ветвях электрической цепи (рисунок 3.53). Расчет токов по рисунку 3.52 для преобразованной части выполним, вычислив величину потенциала узла 11: 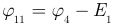 . Токи сторон треугольника вычислим по закону Ома:
. Токи сторон треугольника вычислим по закону Ома:
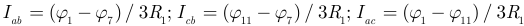
Токи лучей «звезды» вычисляем по первому закону Кирхгофа:
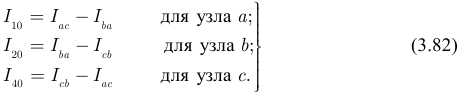
Величину тока 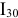 находим из уравнения для узла 11
находим из уравнения для узла 11 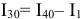 , а величину тока
, а величину тока 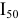 по уравнению для узла 7:
по уравнению для узла 7: 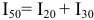 .
.
Последовательность расчета задач методом узловых потенциалов
- Необходимо проставить положительные направления токов в заданной электрической схеме и выполнить упрощение схемы с целью уменьшения числа узлов.
- Пронумеровать узлы, а самый старший узел по номеру «заземлить». Если в схеме содержатся ветви с бесконечной проводимостью и ЭДС, то целесообразно выбирать самый старший узел по номеру, ограничивающему такую ветвь, а потенциал узла на другом конце ветви отличается на величину ЭДС, что приводит к уменьшению общего числа неизвестных потенциалов и, соответственно, к уменьшению количества уравнений в системе. Количество неизвестных потенциалов определяем по формуле
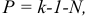
где 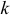 — количество узлов;
— количество узлов; 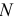 — число ветвей с бесконечной проводимостью.
— число ветвей с бесконечной проводимостью.
- Записываем стандартную систему уравнений и решаем ее относительно неизвестных потенциалов.
- Величины токов определяем по закону Ома для ветви, содержащей ЭДС.
- Возвращаемся к исходной электрической схеме и производим вычисления отдельных токов в ветвях.
- Проверку результатов расчета выполняем подстановкой ответов в уравнения, составленные по законам Кирхгофа или по балансу мощностей.
Таким образом, преимуществом методов контурных токов и узловых потенциалов можно считать меньшее количество уравнений по сравнению с методом непосредственного применения законов Кирхгофа. Если количество уравнений по первому закону Кирхгофа 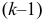 меньше количества уравнений по второму закону Кирхгофа
меньше количества уравнений по второму закону Кирхгофа 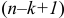 , целесообразно пользоваться методом узловых потенциалов, а если по второму закону Кирхгофа количество уравнений меньше, то целесообразно воспользоваться методом контурных токов.
, целесообразно пользоваться методом узловых потенциалов, а если по второму закону Кирхгофа количество уравнений меньше, то целесообразно воспользоваться методом контурных токов.
Задача 3.12.
Выполнить расчет токов в ветвях электрической цепи (рисунок 3.54), если параметры электрической цепи:
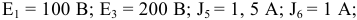
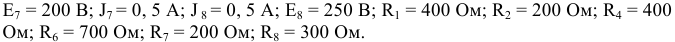
Решение:
На первом этапе выберем направления токов по заданной электрической схеме (рисунок 3.54) и упростим схему. Так
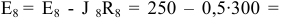
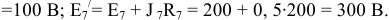
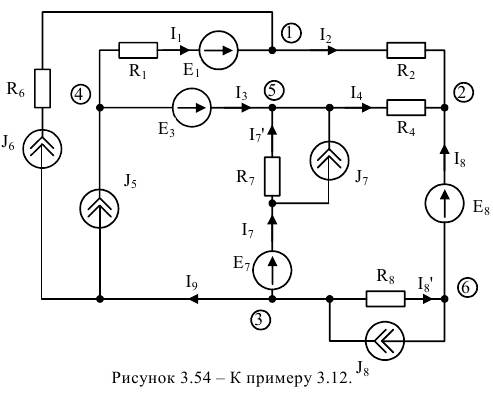
На втором этапе пронумеруем узлы. На рисунке 3.55 представлена упрощенная электрическая схема, содержащая пять узлов и третью ветвь с бесконечной проводимостью, что позволяет самым старшим по номеру выбрать узел,
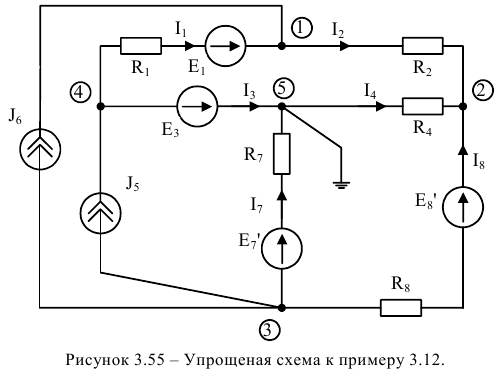
ограничивающий третью ветвь, то есть пятый узел. «Заземляем» пятый узел 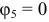 и тогда
и тогда 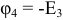 .
.
На третьем этапе составим стандартную систему трех уравнений относительно неизвестных потенциалов узлов 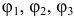 :
:
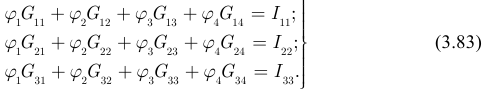
Подставим в систему (3.83) формулы для вычисления коэффициентов, пользуясь известными правилами предыдущего параграфа:
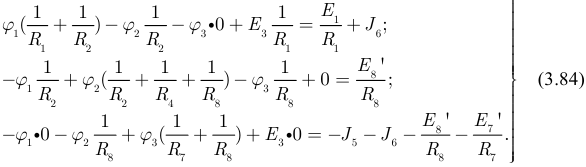
Выполним подстановку параметров элементов в систему (3.84):
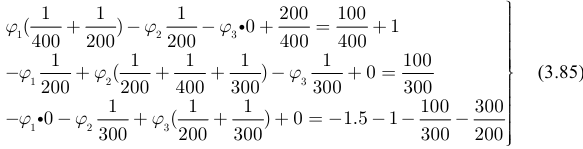
Решаем систему уравнений (3.85) с помощью определителей:
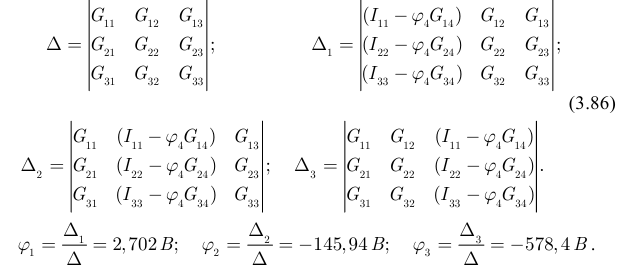
На четвертом этапе рассчитываем величины токов в ветвях схемы рисунка 3.55 по закону Ома:
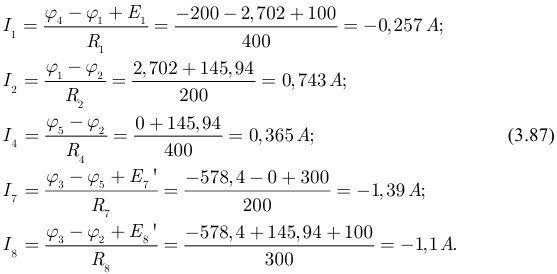
На пятом этапе выполняем расчет остальных токов схемы рисунка 3.54 по первому закону Кирхгофа:
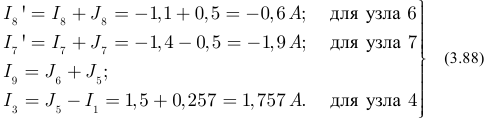
На шестом этапе выполняем проверку результатов расчета для исходной схемы 3.54 по первому закону Кирхгофа:
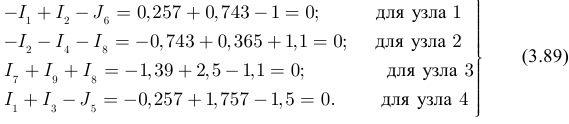
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:

