Основные законы теории электрических цепей
Расчет электрических цепей осуществляют по законам Кирхгофа. Первый закон Кирхгофа вытекает из принципа непрерывности электрического тока: поток вектора полной плотности электрического тока через замкнутую поверхность в любой среде равен нулю:
где
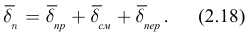
Здесь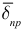 
— плотность тока проводимости; 
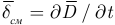, где 
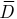— вектор электрической индукции; 
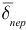— плотность тока переноса зарядов на заряженных телах.
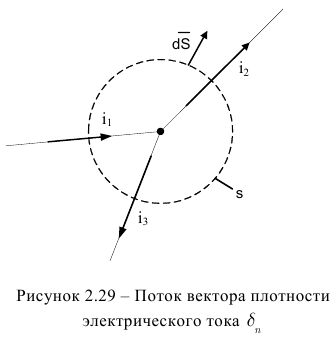
Охватим узел электрической цепи, замкнутой поверхностью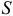 
(рисунок 2.29). Есл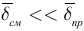и 
и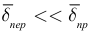 
, то через замкнутую поверхность 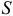проходят только токи проводимости в проводниках, пересекающих эту поверхность.
Согласно закону сохранения электрического заряда и принципа непрерывности тока, в данном случае получим:
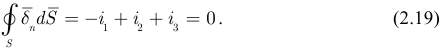
Если число ветвей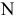 
присоединены к узлу цепи, имеем:
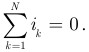
Полученное соотношение называется первым законом Кирхгофа: алгебраическая сумма токов ветвей, пересекающих замкнутую поверхность, равна нулю.
Если внутри замкнутой поверхности находится один единственный узел, то формулировка имеет вид: алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю.
В левой части уравнения следует поставить знак «+» перед буквенными обозначениями токов, положительное направление которых принято от узла, и знак «-» перед буквенным обозначением токов, положительное направление которых принято к узлу. Для случая на рисунке 2.29 перед токам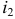и 
и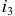 
в уравнении следует поставить «+», а перед током 
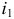знак «-».
Если правую и левую части уравнения умножить на минус единицу, то мы получим знаки перед токами, соответствующие обратному направлению единичного вектора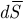 
. Если в результате расчета получено для некоторого тока в некоторый момент времени положительное число, то это указывает, что ток имеет направление согласно стрелке.
Если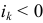 
, то этот ток направлен против стрелки. Второй закон Кирхгофа: алгебраическая сумма ЭДС источников энергии, действующих в ветвях любого замкнутого контура электрической цепи, равна алгебраической сумме падений напряжения в этом же контуре:
где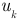 
— падение напряжения на пассивных элементах ветви 
:
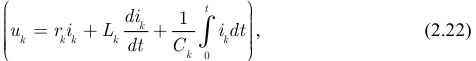
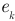— ЭДС 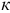-ой ветви.
Здесь: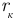 
— сопротивление резистора ветви; 
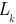— индуктивность катушки ветви; 
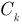— емкость конденсатора ветви.
Для составления уравнений согласно второму закону Кирхгофа предварительно задаются положительные направления токов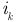 
и ЭДС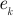 
источников энергии во всех ветвях.
Положительные направления падений напряжения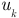 
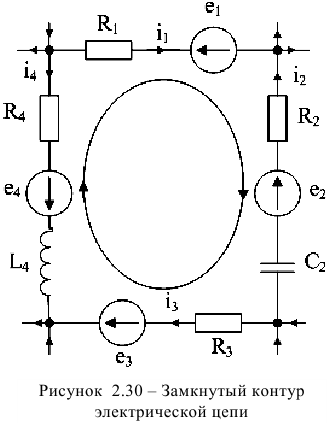
, считаем совпадающими с положительными направлениями токов 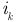. На рисунке 2.30 представлен фрагмент электрической цепи в виде замкнутого контура. Направление обхода контура выбрали произвольно по часовой стрелке. Уравнение по второму закону Кирхгофа имеет вид:
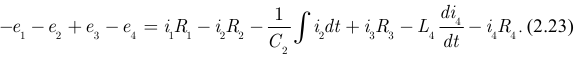
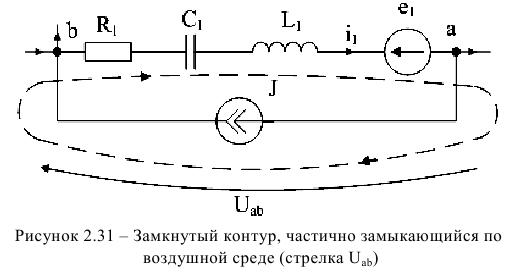
В электрических цепях с сосредоточенными параметрами второй закон Кирхгофа может быть записан и для контура, который проходит частично по элементам электрической цепи и частично проходит от одного узла к другому по окружающему элементы пространству, где мы принимаем отсутствующими магнитные сторонние поля: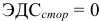 
и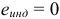 
. Для примера по рисунку 2.31 мы можем составить уравнение:
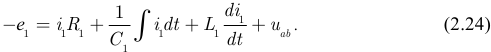
Эта страница взята со страницы задач по электротехнике:
Электротехника — решения задач и примеры выполнения заданий
Возможно эти страницы вам будут полезны:
| Активные идеальные элементы |
| Основные топологические понятия схемы электрической цепи |
| Определение линейных электрических цепей постоянного тока и законы Кирхгофа |
| Закон Ома для ветви, содержащей ЭДС |
