Зарядка, разрядка и саморазрядка конденсатора
Если конденсатор с сопротивлением (утечки)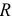 
и емкостью 
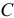подключить к источнику с постоянным напряжением 
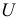(замыканием ключа 
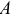), то в цепи (рис. 14.3 а) появится ток зарядки конденсатора:
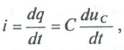
где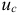 
— напряжение на конденсаторе в любой момент времени переходного процесса.
По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 14.3 а) можно записать уравнение
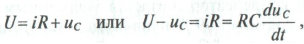
где произведение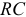 
имеет размерность времени, обозначается буквой т и называется постоянной времени переходного процесса в 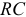-цепи, т. е.
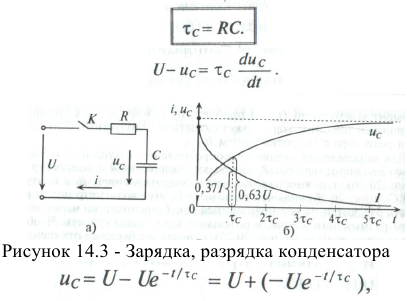
где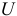 
— установившееся напряжение щ 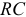-цепи; 
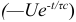— свободная составляющая напряжения 
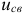на конденсаторе; т.е.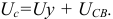 
Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени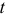 
переходного процесса определяется выражением
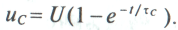
Теоретически зарядка конденсатора длится бесконечно долго, а практически конденсатор считается заряженным, когда напряжение па нем достигает 99 % напряжения источника .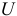
Ток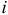 
при зарядке конденсатора уменьшается по закону
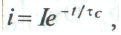
где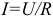 
максимальный ток, который имеет место в начальный момент 
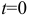зарядки конденсатора (момент коммутации).
За время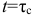 
ток в цепи заряжающегося конденсатора уменьшится до 
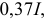а за время 
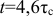— до 
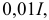при котором переходный процесс можно считать законченным.
Графики изменения напряжения на конденсаторе и тока в цепи зарядки конденсатора изображены на рис. 14.4.
Если конденсатор емкостью 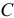, заряженный предварительно до напряжения 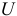, разряжать через резистор с сопротивлением 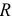(рис. 14.4 а), то напряжение 
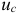на конденсаторе и ток в цепи разрядки будут уменьшаться по закону
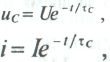
где 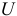— напряжение на конденсаторе до начала разрядки (при 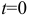), a 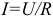максимальный ток в начальный момент разрядки (при ), 
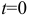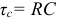— постоянная времени в цепи разрядки конденсатора.
За время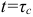 
напряжение и ток уменьшатся до 37 % своих максимальных значений. Изменение напряжения и тока на разряжающемся конденсаторе показаны на рис. 14.4 б (в разных масштабах).
Если конденсатор емкостью 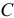, заряженный до напряжения 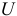, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону 
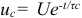. Процесс разрядки конденсатора через свой диэлектрик называется саморазрядом.
Постоянная времени саморазряда зависит от физических свойств диэлектрика
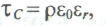
где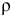 
— удельное сопротивление диэлектрика; 
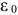— электрическая постоянная; 
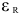— диэлектрическая проницаемость диэлектрика (относительная). Для определения напряжения, тока, ЭДС в любой момент переходного процесса 
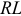-цепи и 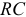-цепи можно воспользоваться таблицей показательных функций.
Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):
Предмет теоретические основы электротехники
Возможно эти страницы вам будут полезны:
