Проводимость, расчет электрических цепей методом проводимостей
Для расчета сложных электрических цепей, и в особенности цепей переменного тока, целесообразно вместо сопротивления использовать проводимость.
Проводимость в цепи постоянного тока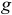 
— величина, обратная сопротивлению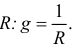 
В цепях переменного тока, как известно, существует три типа сопротивлений: активное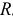 
, реактивное 
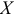и полное 
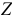. По аналогии с этим введено и три типа проводимостей: активная 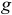, реактивная 
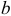и полная 
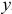. Однако только полная проводимость 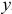является величиной, обратной полному сопротивлению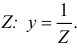 
Для введения активной 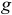и реактивной 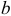проводимостей рассмотрим цепь переменного тока из последовательно соединенных активного 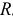и индуктивного 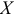сопротивлений (рис. 10.4 а).
Построим для нее векторную диаграмму (рис. 10.4 6). Ток в цепи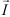 
разложим на активную 
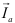и реактивную 
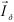составляющие и от полученного треугольника токов перейдем к треугольнику сопротивлении (рис. 10.4 в). Из последнего имеем:
где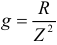 
— активная проводимость,
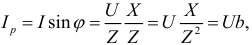
где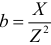 
— реактивная проводимость.
Теперь установим взаимосвязь между проводимостями. Для рассматриваемой цепи имеем:
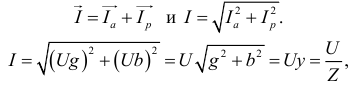
где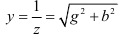 
— полная проводимость цепи.
По аналогии с треугольником сопротивлений (рис. 10.5 в) строим треугольник проводимостей (рис. 10.5 г). По аналогии с индуктивным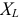 
и емкостным 
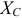сопротивлениями различают индуктивную 
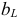и емкостную 
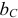проводимости.
Если в цепи больше двух параллельных ветвей, то для рационального расчета используется метод проводимостей, который основан на следующем.
1)Ток в каждой цепи является векторной суммой активной и реактивной составляющих (рис. 10.5).
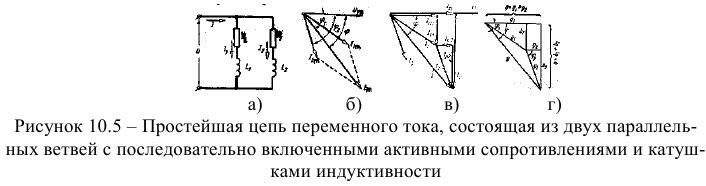
Например, для рассмотренной выше цепи действующие значения токов в ветвях можно рассчитать по следующим формулам: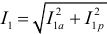 
, 
.
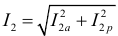2) Активные составляющие совпадают по фазе с напряжением и равны:
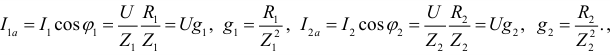
где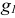 
и 
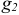— активные проводимости первой и второй ветвей.
3) Реактивные составляющие токов отличаются по фазе от напряжения на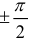 
и рассчитываются по формулам:
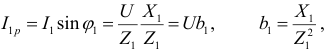
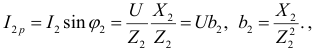
где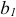 
и 
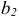— реактивные проводимости первой и второй ветвей. Тогда: 
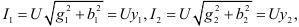где 
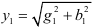и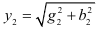 
— полные проводимости обоих ветвей.
Проводимость всей цепи может быть рассчитана по формуле представлена треугольником проводимостей (рис.3.28г), который является следствием векторной диаграммы токов: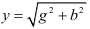 
, где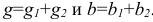 
4)Общая сила тока в цепи может быть рассчитана как модуль векторной суммы активной и реактивной составляющих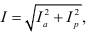 
где 
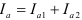и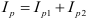 
.
5)Сдвиг фаз между током и напряжением: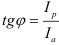 
или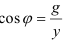 
.
6)Активную, реактивную и полную мощность цепи можно рассчитать по формулам:
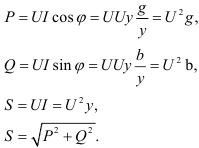
0.3 Взаимная индуктивность. Согласное, встречное включения катушек
Поток самоиндукции первой катушки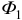 
, можно разделить на два: поток рассеяния 
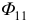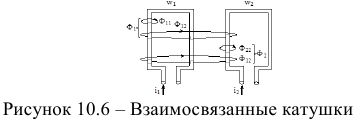
сцепляющийся только с катушкой 1 и поток взаимоиндукции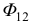 
, сцепляющийся также со второй катушкой (рис. 10.6). 
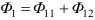. Аналогично для второй катушки :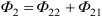 
Полное потокосцепление первой катушки:
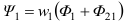
на рисунке поток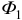и и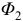 
направлены одинаково, говорят «согласно». Поэтому в скобках перед 
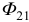стоит (+).
Если изменить направление тока в катушке 2, то потоки будут направлены встречно и будет знак(-). В общем случае: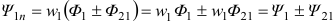 
(+) — согласное , (-) — встречное. 
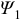— потокосцепление самоиндукции, 
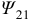— потокосцепление взаимоиндукции. Величина 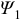пропорциональна 
:
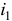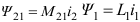
где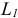 
— индуктивность первой катушки; 
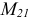— взаимная индуктивность. Аналогично для второй катушки: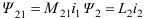 
Полная ЭДС, индуктированная в первом контуре:
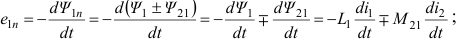
Явление наведения ЭДС в каком-либо контуре при изменение тока в другом контуре, называется взаимоиндукцией.
Наведённую ЭДС называют ЭДС взаимоиндукции и обозначают:
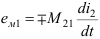— ЭДС взаимоиндукции в первой катушке,
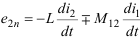— ЭДС взаимоиндукции во второй катушке.
В этих формулах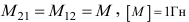 
Степени индуктивной связи катушки определяются с помощью коэффициентов связи:
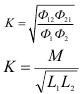
Поскольку у реальных катушек всегда существуют потоки рассеяния, то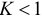 
.
При расчёте таких цепей необходимо учитывать, как направлены потоки маг-нитносвязанных катушек — согласно или встречно.
Направления потоков можно определить, зная направление намотки катушек на сердечнике и направление тока в катушках (рис. 10.7).
Токи, входящие в одноимённые зажимы магнитосвязанных катушек, дают согласное направление магнитных потоков в этих катушек.
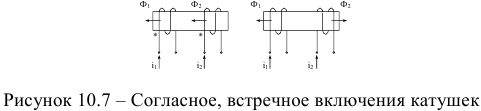
Одноимённые зажимы помечают либо точкой, либо звёздочкой. Если на принципиальной электрической схеме токи ориентированы одинаково относительно одноимённых зажимов катушек, то это согласное включение катушек, иначе — встречное.
Эта страница взята со страницы лекций по предмету теоретические основы электротехники (ТОЭ):
Предмет теоретические основы электротехники
Возможно эти страницы вам будут полезны:
| Резонанс напряжений |
| Цепь с активным сопротивлением, индуктивностью и емкостью |
| Коэффициент мощности |
| Ток, напряжение, сопротивление и мощность в комплексном виде |
