Задача №17
Диск массой 2,0 кг, радиусом 10 см вращается с частотой 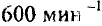 вокруг горизонтальной оси, проходящей через его центр. Через 20 с. под действием постоянного тормозящего момента диск остановился. Считая массу диска равномерно распределенной, найти тормозящий момент и число оборотов, которое сделает диск до полной остановки.
вокруг горизонтальной оси, проходящей через его центр. Через 20 с. под действием постоянного тормозящего момента диск остановился. Считая массу диска равномерно распределенной, найти тормозящий момент и число оборотов, которое сделает диск до полной остановки.
Дано:
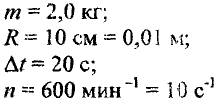
Найти: 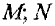
Решение:
Дня определения тормозящего момента 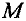 сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения. Запишем его в виде
сил, действующих на тело, нужно применить основное уравнение динамики вращательного движения. Запишем его в виде
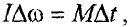
где 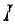 — момент инерции диска относительно оси, проходящей через центр масс;
— момент инерции диска относительно оси, проходящей через центр масс;
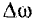 — изменение угловой скорости за промежуток времени
— изменение угловой скорости за промежуток времени 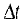 .
.
По условию задачи
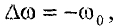
где 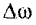 — начальная угловая скорость, так как конечная угловая скорость
— начальная угловая скорость, так как конечная угловая скорость 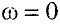 .
.
Выразим начальную угловую скорость через частоту вращения диска. Тогда
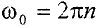 и
и 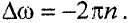
Момент инерции диска относительно оси, перпендикулярной плоскости диска и проходящей через его центр масс:
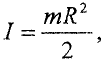
где 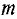 — масса диска;
— масса диска;
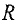 — его радиус.
— его радиус.
Тогда формула (6.5) примет вид
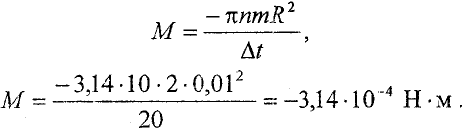
Знак минус в (6.6) указывает на то, что на диск действует тормозящая сила.
Угол поворота за время вращения диска до остановки может быть определен как
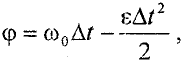
где 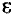 — угловое ускорение.
— угловое ускорение.
По условию задачи, 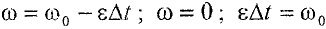 . Тогда из (6.7) следует, что
. Тогда из (6.7) следует, что
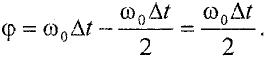
Так как

то число полных оборотов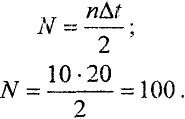
Ответ. 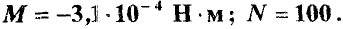
Эта задача взята со страницы задач по физике с решением:
Возможно эти задачи вам будут полезны:

