Задача №12
Тело массой 1,0 кг под действием силы движется прямолинейно. Зависимость модуля перемещения тела от времени задана уравнением 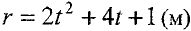 . Определить работу
. Определить работу
силы за 10 с от начала ее действия и зависимость кинетической энергии от времени.
Дано: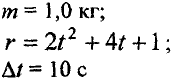
Найти: 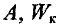
Решение:
Работа, совершаемая силой:
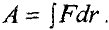
По второму закону Ньютона сила, действующая на тело:
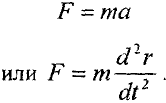
Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени. В соответствии с этим
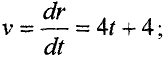
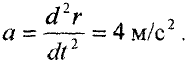
Тогда из (4.4) и (4.6) имеем
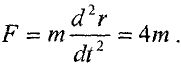
Из выражения (4.5) находим
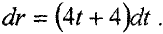
Подставив (4.7) и (4.8) в (4.3) вычисления 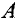 , получим (4.6) (4.7) (4.8)
, получим (4.6) (4.7) (4.8)
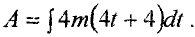
По этой формуле вычислим работу, совершаемую силой за 10 с с начала ее действия:
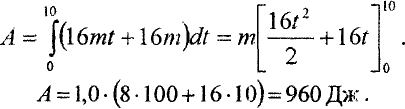
Кинетическая энергия тела
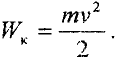
Подставляя (4.3) в формулу (4.9), имеем
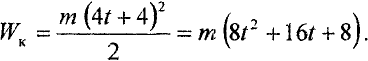
Ответ. 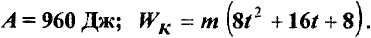
Эта задача взята со страницы задач по физике с решением:
Возможно эти задачи вам будут полезны:

