Задача №3 Ускорение материальной точки изменяется по закону 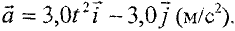Найти, на каком расстоянии от начала координат точка будет находиться в момент времени.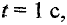

Задача №3

Ускорение материальной точки изменяется по закону Найти, на каком расстоянии от
начала координат точка будет находиться в момент времени если при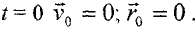

Дано: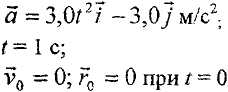

Найти: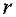

Решение:

Разложим вектор скорости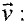

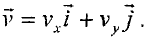
Так как компоненты вектора скорости 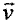связаны с компонентами вектора ускорения соотношениями

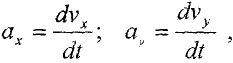
то, учитывая, что по условию задачи 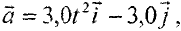можем записать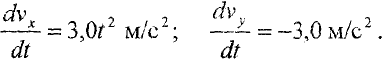

Разделим переменные и проинтегрируем

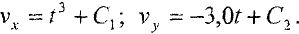
Найдем постоянные интегрирования, исходя из начальных услови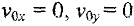й при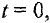

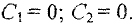
Так как компоненты вектора скорости 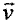связаны с компонентами радиус-вектора 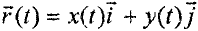соотношениями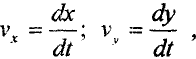

то получаем два дифференциальных уравнения

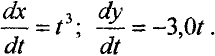
Тогда координаты 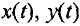получаются интегрированием выражений (1.1)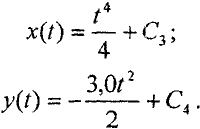

Учитывая начальные условия: 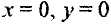при 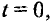находим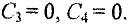
Уравнение движения материальной точки будет иметь вид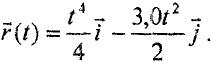

Модуль радиус-вектора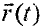

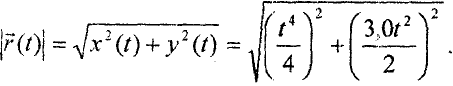
Подставляя время 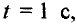получим расстояние 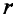от начала координат до материальной точки:

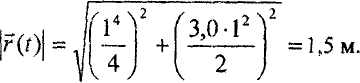
Ответ.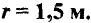

Эта задача взята со страницы задач по физике с решением:

Решение задач по физике

Возможно эти задачи вам будут полезны:

Задача №1 Уравнение движения материальной точки имеет вид , где Найти координату, проекции скорости и ускорения точки в момент времени.

Задача №2 С башни в горизонтальном направлении брошено тело с начальной скоростью Пренебрегая сопротивлением воздуха, определить для момента времени с после начала движения: 1) скорость тела: 2) радиус кривизны его траектории.

Задача №4 Тело вращается вокруг неподвижной оси по закону (рад), где рад; рад/с; . Расстояние от точки до оси вращения . Найти полное ускорение материальной точки в момент времени.

Задача №5 Диск радиусом вращается вокруг неподвижной оси так. что зависимость угловой скорости от времени задается уравнением (рад/с), где Определить для точек на ободе диска к концу первой секунды после начала движения: 1) модуль полного ускорения; 2) число оборотов, сделанных диском.