Траектория
Траектория — это линия (или, как принято говорить, кривая), которую описывает тело при движении относительно выбранного тела отсчёта.
Говорить о траектории имеет смысл лишь в том случае, когда тело можно представить в виде материальной точки.
Траектории могут иметь разную форму. О форме траектории иногда удаётся судить по видимому следу, который оставляет движущееся тело, например, летящий самолёт или проносящийся в ночном небе метеор.
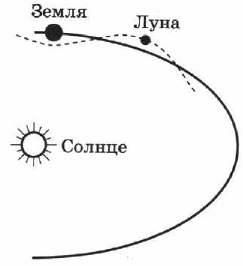
Форма траектории зависит от выбора тела отсчёта. Например, относительно Земли траектория движения Луны представляет собой окружность, относительно Солнца — линию более сложной формы (рис. 2). При изучении механического движения в качестве тела отсчёта, как правило, рассматривается Земля.
Способы задания положения точки и описание её движения.
Положение точки в пространстве задаётся двумя способами: 1) с помощью координат; 2) с помощью радиус-вектора.
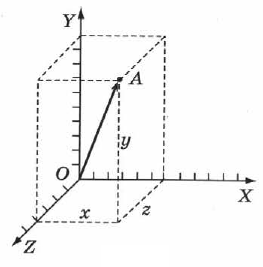
Положение точки с помощью координат задаётся тремя проекциями точки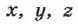 
на оси декартовой системы координат 
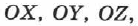связанные с телом отсчёта (рис. 3). Для этого из точки 
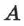необходимо опустить перпендикуляры на плоскости 
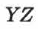(координата 
), 
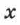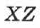(координата 
), 
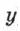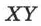(координата 
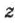) соответственно. Записывается это так: 
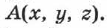Для конкретного случая, изображённого на рис. 3 
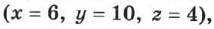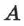точка обозначается 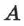(6; 10; 4,5).
Если точка движется в пределах некоторой плоскости, то через выбранные на теле отсчёта точки достаточно провести две координатные ос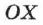и: 
и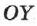 
. Тогда положение точки на плоскости определяют двумя координатам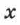и — и 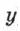(рис. 4).
Если точка движется вдоль прямой, достаточно задать одну координатную ось 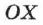и направить её вдоль линии движения.
Задание положения точки 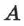с помощью радиус-вектора осуществляется соединением точки 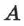с началом координат 
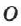(рис. 3). Направленный отрезок 
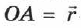называется радиус-вектором.
Радиус-вектор — это вектор, соединяющий начало отсчёта с положением точки в произвольный момент времени.
Точка задана радиус-вектором, если известны его длина (модуль) и направление в пространстве, т. е. значения его проекций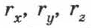 
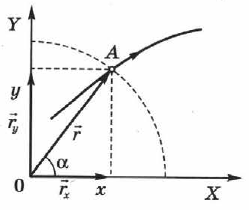
на оси координат 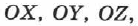либо углы между радиус-вектором и осями координат. Для случая движения на плоскости (рис. 4) имеем:
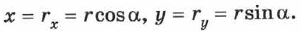
Здесь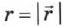 
— модуль радиус-вектора 
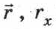и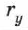 
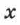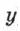— его проекции на оси координат, все три величины — скаляры; и — координаты точки .
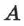Последние уравнения демонстрируют связь между координатным и векторным способами задания положения точки.
Вектор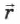 
можно также разложить на составляющие по осям 
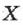и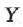 
, т. е. представить в виде суммы двух векторов (рис. 4):
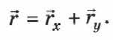
Таким образом, положение точки в пространстве задаётся либо её координатами, либо радиус-вектором.
В соответствии со способами задания координат движение точки можно описать: 1) координатным способом; 2) векторным способом.
При координатном способе описания (или задания) движения изменение координат точки со временем записывается в виде функций всех трёх её координат от времени:
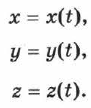
Уравнения (1.1) называют кинематическими уравнениями движения точки, записанными в координатной форме. Зная кинематические уравнения движения и начальные условия (т.е. положение точки в начальный момент времени), можно определить положение точки в любой момент времени.
При векторном способе описания движения точки изменение её положения со временем задаётся зависимостью радиус-вектора от времени:
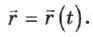
Уравнение (1.2) представляет собой уравнение движения точки, записанное в векторной форме. Если оно известно, то для любого момента времени можно рассчитать радиус-вектор точки, т. е. определить её положение (как и в случае с координатным способом). Таким образом, задание трёх скалярных уравнений (1.1) равносильно заданию одного векторного уравнения (1.2).
Для каждого случая движения вид уравнений (1.1) или (1.2) будет вполне определенным. Если траекторией движения точки является прямая линия, движение называется прямолинейным, а если кривая — криволинейным.
Эта лекция взята со страницы лекций по всем темам предмета физика:
Возможно эти страницы вам будут полезны:
| Система отсчёта в физике |
| Поступательное движение в физике |
| Перемещение и путь в физике |
| Скорость в физике |
