Оглавление:
Сравнение результатов двух методов количественного анализа
Методами математической статистики можно сравнить выборочные совокупности (выборки) по воспроизводимости (сравнение дисперсий) и правильности (сравнение средних).
Сравнение двух выборочных дисперсий проводят, когда результаты получены двумя разными методами, в двух лабораториях, на двух приборах, двумя аналитиками и т. д. При сравнении сначала находят дисперсии 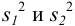 (или, соответственно,
(или, соответственно, 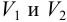 ) для соответствующих выборок с
) для соответствующих выборок с 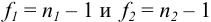 .
.
Для ответа на вопрос, значимо или незначимо отличаются дисперсии, проводят сравнение с табличным значением критерия Фишера 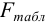 вычисленного значения критерия Фишера —
вычисленного значения критерия Фишера — 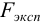 .
.
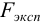 вычисляют по формуле, деля большую дисперсию на меньшую:
вычисляют по формуле, деля большую дисперсию на меньшую:
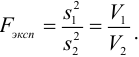
Значения 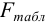 можно взять из табл. 10 приложения. В этой таблице число степеней свободы
можно взять из табл. 10 приложения. В этой таблице число степеней свободы 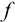 большей дисперсии находится в горизонтальном ряду. Если
большей дисперсии находится в горизонтальном ряду. Если 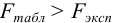 при Р = 0,95 (или Р = 0,99), расхождение между выборками незначимо, дисперсии однородны.
при Р = 0,95 (или Р = 0,99), расхождение между выборками незначимо, дисперсии однородны.
Сравнение средних результатов двух выборок проводят, если проверка их по критерию Фишера указывает на незначимость расхождения дисперсий, т.е. на одинаковую воспроизводимость результатов сравниваемых выборок. Для сравнения используют t -распределение. Сначала рассчитывают средневзвешенную дисперсию 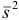 (или
(или 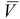 ) по формуле:
) по формуле:
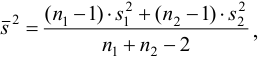
затем вычисляют 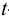 -критерий:
-критерий:
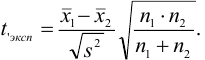
Сравнивают 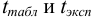 при числе степеней свободы
при числе степеней свободы 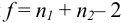 и доверительной вероятности Р = 0,99 (или уровне значимости
и доверительной вероятности Р = 0,99 (или уровне значимости 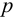 = 0,01).
= 0,01).
Если 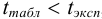 то расхождение значимо. Если
то расхождение значимо. Если 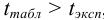 то расхождение между средними двух выборок незначимо, и результаты можно рассматривать как одну выборочную совокупность с
то расхождение между средними двух выборок незначимо, и результаты можно рассматривать как одну выборочную совокупность с 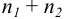 количеством результатов.
количеством результатов.
Пример 9.6.
Определите, существует ли значимое различие между выборочным средним значением результатов определения массовой доли серы в каменном угле (%): 2,10; 2,12; 2,13; 2,15; 2,15 и средним генеральной совокупности (истинным значением) 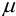 = 2,15 %, полученным для
= 2,15 %, полученным для 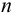 = 80.
= 80.
Решение:
Найдем среднее для выборки и стандартное отклонение отдельных результатов:
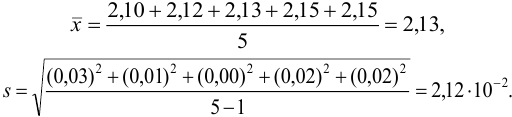
Как в примере 9.4, находим значение величины 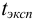 :
:
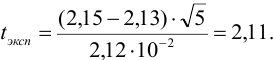
Сравниваем 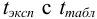 коэффициента Стыодента (табл. 8 приложения), значение которого при
коэффициента Стыодента (табл. 8 приложения), значение которого при 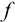 = 4 и Р = 0,95 равно 2,78. Поскольку полученное среднее значение
= 4 и Р = 0,95 равно 2,78. Поскольку полученное среднее значение 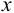 не отличается значимо от истинного значения
не отличается значимо от истинного значения 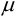 (среднего генеральной совокупности), делаем вывод о вероятном отсутствии систематической погрешности.
(среднего генеральной совокупности), делаем вывод о вероятном отсутствии систематической погрешности.
Пример 9.7.
Массовую долю (%) 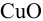 в минерале определили методом иодометрии и методом комплексонометрии. По первому методу получили результаты: 38,20; 38,00; 37,66. По второму 37,70; 37,65; 37,55. Значимо ли различаются результаты данных методов?
в минерале определили методом иодометрии и методом комплексонометрии. По первому методу получили результаты: 38,20; 38,00; 37,66. По второму 37,70; 37,65; 37,55. Значимо ли различаются результаты данных методов?
Решение:
Вычислим среднее значение для каждого метода:
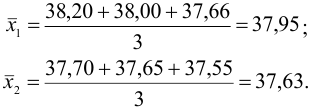
Рассчитаем дисперсии:
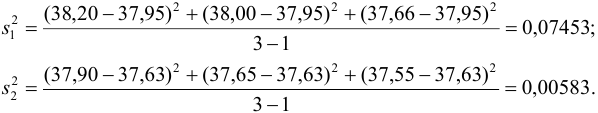
Вычислим критерий Фишера (9.3):
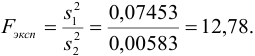
Для сравнения дисперсий сопоставим значение 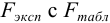 (табл. 10 приложения) при Р = 0,95 и
(табл. 10 приложения) при Р = 0,95 и 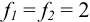 . Значение
. Значение 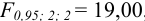 , т. е.
, т. е.
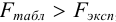 , следовательно, расхождение между дисперсиями незначимо и воспроизводимость результатов, полученных по двум методикам, одинакова.
, следовательно, расхождение между дисперсиями незначимо и воспроизводимость результатов, полученных по двум методикам, одинакова.
Показав незначимость расхождения дисперсий, можно провести сравнение средних. Для этого рассчитаем среднее взвешенное двух дисперсий (9.4):
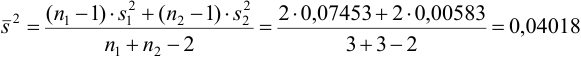
и с помощью  -критерия (9.5) оценим расхождение между средними
-критерия (9.5) оценим расхождение между средними 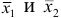 двух методик:
двух методик:
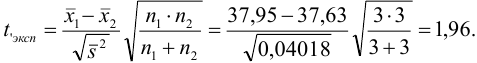
Сопоставляем полученное значение 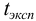 .и с табличным
.и с табличным 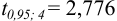 (при Р = 0,95 и/= 3 + 3 — 2 = 4). Так как
(при Р = 0,95 и/= 3 + 3 — 2 = 4). Так как 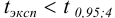 , то различие между х, и х2 незначимо. Следовательно, все результаты обоих методов отражают истинное содержание
, то различие между х, и х2 незначимо. Следовательно, все результаты обоих методов отражают истинное содержание 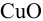 в минерале. Поэтому данные анализа по двум методикам могут быть объединены и представлены в виде:
в минерале. Поэтому данные анализа по двум методикам могут быть объединены и представлены в виде:
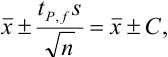
где 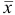 — среднее из всех
— среднее из всех 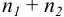 результатов.
результатов.
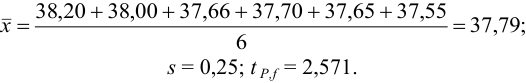
Результат анализа: 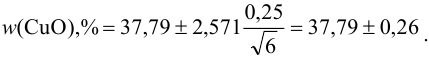
Следует заметить, что сравнение двух выборок методами математической статистики рекомендуется проводить при 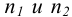 более 10. Поэтому пример 9.7, скорее, иллюстрирует схему расчета.
более 10. Поэтому пример 9.7, скорее, иллюстрирует схему расчета.
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы:

