Оглавление:
Классификация и оценка погрешностей количественного анализа
По способу вычисления различают абсолютную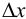 
и относительную 
(ранее 
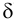) погрешности.
Если среднее арифметическое значение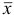 
для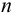 
полученных результатов анализа составляет:
то абсолютную погрешность выражают как
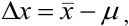
где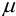 
— истинное содержание определяемого компонента (например, известное для стандартного образца или контрольной пробы). Очевидно, что абсолютная погрешность может быть положительной или отрицательной, в зависимости от того, каким получился результат: завышенным или заниженным по сравнению с истинным (рис. 9.1).
Относительная погрешность может быть выражена в долях или процентах и обычно не имеет знака:
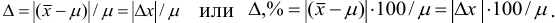
По происхождению погрешности делят на систематические, случайные и промахи (грубые ошибки).
Погрешность определения, обусловленная постоянно действующей причиной, неизменная во всех измерениях, сохраняющая знак от опыта к опыту или закономерно изменяющаяся, называется систематической погрешностью. Погрешность, случайным образом изменяющаяся от опыта к опыту, называется случайной погрешностью. Грубые погрешности или промахи резко искажают результат анализа, вызываются небрежностью и обычно легко обнаруживаются.
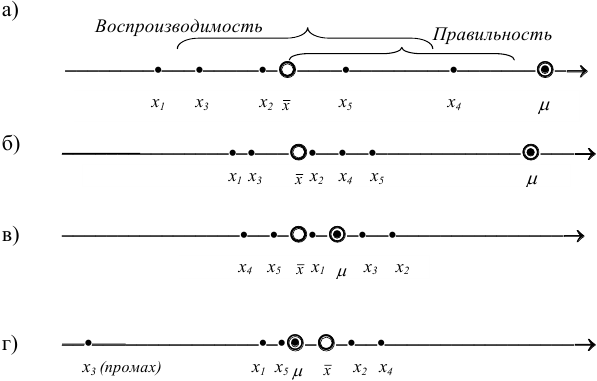
Рис. 9.1. Воспроизводимость и правильность химического анализа. Результаты: а) невоспроизводимы и неправильны; б) воспроизводимы, но неправильны; в) воспроизводимы и правильны; г) воспроизводимы и правильны, но есть промах.
С систематическими погрешностями связана правильность анализа, со случайными погрешностями — воспроизводимость. Правильность и воспроизводимость являются метрологическими характеристиками анализа и входят в понятие «точность анализа».
Воспроизводимость результатов анализа характеризует рассеяние единичных результатов относительно среднего.
Правильность характеризует отклонение полученного результата от истинного и показывает, насколько близка к нулю систематическая погрешность. Систематические погрешности выявляют и устраняют. Если же устранение невозможно, то при постоянном значении систематической погрешности ее учитывают, вводя поправку. Для выявления используют различные приемы и методы, например “введено — найдено”, анализ стандартного образца, “двойной или тройной добавки”.
Оценка случайных погрешностей проводится методами математической статистики. В обычной практике выполняют ограниченное число параллельных измерений п (обычно 3-5), называемое выборочной совокупностью данных или просто выборкой (в отличие от генеральной совокупности — при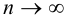 
). При 
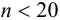математическую обработку результатов проводят с использованием распределения Стьюдепта, связывающего вероятность попадания величины в данный доверительный интервал и объем выборки 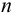. Среднее для ряда параллельных определений, 
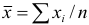, является наиболее вероятным значением измеряемой величины.
Характеристики случайной погрешности (воспроизводимости) для выборки: выборочная дисперсия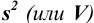 
, стандартное отклонение 
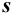и относительное стандартное отклонение 
:
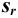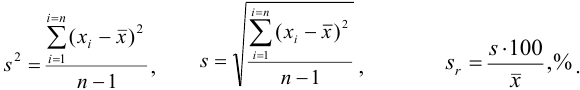
С ними связаны дисперсия среднего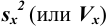 
и стандартное отклонение среднего 
: 
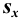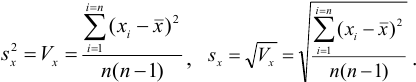
При обработке данных химического анализа определяют границы доверительного интервала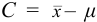 
, вводя число степеней свободы 
.
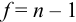Доверительный интервал (С) — это интервал значений, в котором для данного вида распределения случайных величин (при отсутствии систематических погрешностей), при заданной доверительной вероятности Р и числе степеней свободы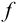 
лежит истинное значение определяемой величины:
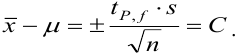
Доверительная вероятность попадания величины внутрь доверительного интервала в химическом анализе принята равной 0,95 или 95 %. Это означает, что в рассчитанный интервал попадут 95 из 100 значений. Коэффициенты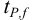 
— коэффициенты нормированных отклонений Стьюдента приведены в табл. 8 приложения. Зависимость 
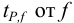показывает, что с возрастанием числа степеней свободы, т. е. числа параллельных результатов, увеличивается и точность анализа, поскольку доверительный интервал характеризует воспроизводимость и, в какой-то мере, правильность результатов химического анализа. С учетом доверительного интервала истинное значение представляют выражением:
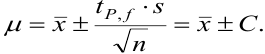
Оценка промахов (выбраковка результатов). Перед обработкой данных методами математической статистики необходимо выявить промахи и исключить их из числа обрабатываемых результатов. Для выявления промахов используют различные критерии, в частности,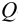 
-критерий. Проверку соответствия 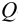-критерию про водят следующим образом. Все параллельные результаты располагают в последовательности их убывания или возрастания. При этом 
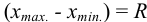— размах варьирования. Затем рассчитывают 
:
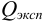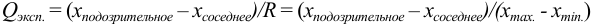
и сравнивают с критическим значением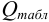 
при доверительной вероятности 0,90 (табл. 9 приложения).
Если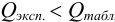 
, то промах отсутствует и подозрительный результат оставляют в составе выборки. Если же 
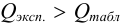, то подозрительное значение является промахом, грубой погрешностью; его отбрасывают.
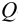— критерий рекомендуется применять к выборкам с 
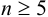. При малой выборке 
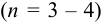заметно отличающийся от других результат просто отбрасывают, а определение повторяют и после этого оценивают случайную погрешность. Если 
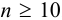, промахи можно установить с помощью 
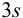— критерия, проверяя для каждого отклонения 
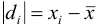выполнение условия 
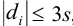, позволяющего оставить результат в составе выборки.
Пример 9.1.
Контрольный раствор соли кальция имеет концентрацию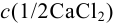 
, равную 0,1056 моль/л. Студентом было получено методом перманганатометрии среднее значение 
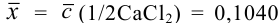. Вычислите абсолютную и относительную погрешности.
Решение:
Абсолютная погрешность результата:
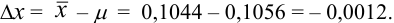
Относительная погрешность:
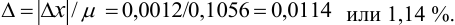
Пример 9.2.
При определении содержания аскорбиновой кислоты в пробе картофеля по новой методике пробоподготовки получены следующие результаты (мг/100 г): 14,50; 14,43; 14,54; 14,45; 14,44; 14,52; 14,58; 14,40; 14,25; 14,49. Оцените:
а) наличие грубых погрешностей (промахов);
б) воспроизводимость результатов анализа.
Решение:
а) наличие промахов оценим по 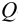-критерию. Представим экспериментальные данные в порядке возрастания: 14,25; 14,40; 14,43; 14,44; 14,45; 14,49; 14,50; 14,52; 14,54; 14,58. Проверим подозрительные значения 14,25 и 14,58. Вычислим 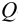— критерий для этих величин:
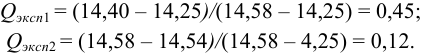
Из табл. 9 приложения при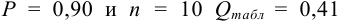 
; 
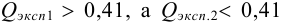, следовательно, значение 14,25 недостоверно и его исключаем, сокращая объем выборки до 
.
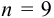б) после исключения промаха найдем среднее и характеристики воспроизводимости: дисперсию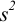 
, стандартное отклонение 
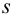и относительное стандартное отклонение 
:
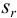Пример 9.3.
Используя условия примера 9.2 и считая, что содержание аскорбиновой кислоты для той же пробы картофеля, определенное по стандартной методике составляет 14,58 мг/100 г, рассчитайте доверительный интервал и установите, свидетельствуют ли полученные результаты о наличии систематической погрешности при работе по новой методике?
Решение:
Для расчета доверительного интервала при числе степеней свободы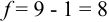 
и доверительной вероятности Р = 0,95 из табл. 8 приложения находим коэффициент Стьюдента 
.
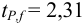Находим полуширину доверительного интервала, оставляя значащие цифры:
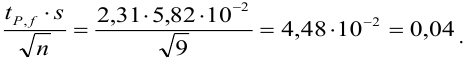
Таким образом, среднее содержание аскорбиновой кислоты лежит в границах
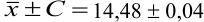или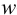 
(кислоты), мг/100 г = 14,48 ± 0,04. Истинное значение содержания аскорбиновой кислоты14,58 не попадает в доверительный интервал, следовательно, такой метод пробоподготовки картофеля к анализу имеет систематическую погрешность, причину которой надо выяснять.
Пример 9.4.
При анализе стандартного образца, содержащего 1,44 %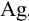 
, были получены результаты (%): 1,31; 1,45; 1,42; 1,32; 1,30. Определить стандартное отклонение, доверительный интервал и сделать выводы о наличии систематической погрешности в использованном методе определения серебра.
Решение:
Проверим наличие грубых погрешностей по 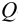-критерию. Располагаем экспериментальные данные в порядке возрастания численных значений: 1,30; 1,31; 1,32; 1,42; 1,45. Предполагаем, что значение 1,45 является результатом грубой погрешности. Рассчитываем для него 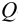-критерий:
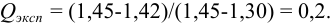
Для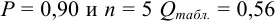 
(табл. 9 приложения). Вычисленное значение 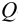-критерия 
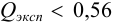, следовательно, грубая погрешность отсутствует.
Находим среднее значение из пяти определений:
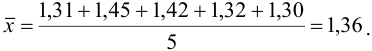
Вычисляем стандартное отклонение:
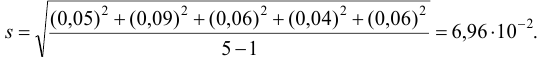
По табл. 8 приложения для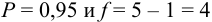 
находим 
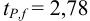и рассчитываем полуширину доверительного интервала для 
:
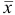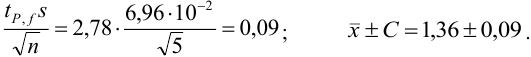
Результат представляем в виде: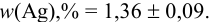 
Наличие систематической погрешности можно выявить, как в предыдущем примере, проверяя попадает ли истинное значение содержания серебра в доверительный интервал. В данном случае для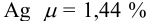 
попадает в границы доверительного интервала, следовательно, систематическая погрешность в этом методе определения серебра отсутствует.
Ответить на вопрос задачи о присутствии систематической погрешности можно, используя критерий Стьюдента и сравнивая вычисленное значение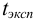 
с табличным значением 
— критерия при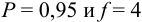 
, равным 2,78:
Поскольку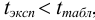 
делаем вывод о вероятном отсутствии систематической погрешности.
Пример 9.5.
При определении ванадия были получены результаты: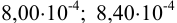 
г. Чему равен доверительный интервал? Сколько параллельных определений необходимо провести для достижения доверительного интервала с полушириной
?
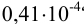Решение:
Находим среднее значение:
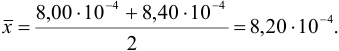
Вычислим стандартное отклонение:
По табл. 8 приложения находим 
и вычисляем полуширину доверительного интервала:
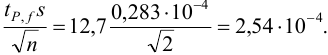
Требуется же получить доверительный интервал с полушириной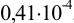 
Найдем необходимое для этого соотношение 
:
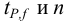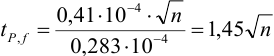или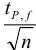 
должно быть 
.
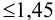При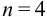 
значение критерия 
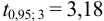, а отношение 
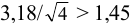; при 
значение критерия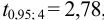 
, а отношение 
.
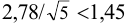Таким образом, для сужения границ доверительного интервала до 
необходимо провести 5 параллельных определений.
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы:
