Оглавление:
Расчеты с использованием ЭДС гальванического элемента
При проведении подобных расчетов используются два уравнения Нернста с разными редокс- парами или разными концентрациями компонентов редокс- пар. В свою очередь, концентрация компонентов редокс- пары может быть связана с любым видом взаимодействий в растворе из рассматриваемых в главах 2,3,6 и разделах 5.2-5.3. Расчеты с использованием ЭДС гальванического элемента приближают к пониманию изучаемого в дальнейшем потенциометрического метода анализа.
Пример 5.20.
Приведите схему и вычислите ЭДС гальванического элемента, составленного из редокс- пар 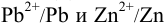 при стандартных активностях всех участников и константу равновесия, протекающей в нем окислительно-восстановительной реакции.
при стандартных активностях всех участников и константу равновесия, протекающей в нем окислительно-восстановительной реакции.
Решение:
Справочные данные:
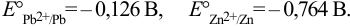
В гальваническом элементе должна протекать самопроизвольная реакция с 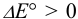 (разд. 5.1). Для этого катодом должен быть свинцовый электрод, анодом — цинковый.
(разд. 5.1). Для этого катодом должен быть свинцовый электрод, анодом — цинковый.
Схема гальванического элемента:
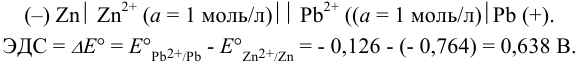
По формуле (5.11) находим для реакции:
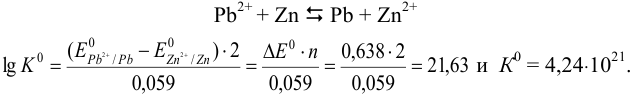
Пример 5.21.
Приведите схему гальванического элемента, определите его ЭДС и константу протекающей в нем реакции. Элемент состоит из свинцового полуэлемента (свинцовой пластинки, погруженной в раствор, содержащий взвесь 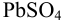 в 0,10 М
в 0,10 М 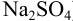 ), цинкового полуэлемента (цинковой пластинки в 0,020 М растворе
), цинкового полуэлемента (цинковой пластинки в 0,020 М растворе 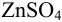 ) и солевого мостика с
) и солевого мостика с 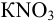 .
.
Решение:
Рассматривая стандартные потенциалы редокс-пар 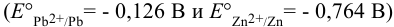 , можем установить катод и анод в данном гальваническом элементе согласно раздела 5.1 (см. также пример 5.20): сила
, можем установить катод и анод в данном гальваническом элементе согласно раздела 5.1 (см. также пример 5.20): сила 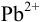 как окислителя выше, чем
как окислителя выше, чем 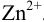 , значит цинковый полуэлемент — анод, а свинцовый — катод.
, значит цинковый полуэлемент — анод, а свинцовый — катод.
Схема элемента:
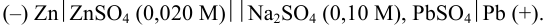
Полуреакция на аноде: 1) 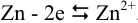 , а в катодном полуэлементе совокупность реакций:
, а в катодном полуэлементе совокупность реакций:
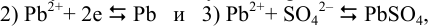
приводящих (разд. 5.3.4) к полуреакции:
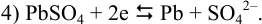
Вычислим, пренебрегая влиянием ионной силы и учитывая связывание 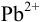 в малорастворимое соединение, потенциалы соответствующих электродов по уравнению Нериста (см. формулы (5.3) и (5.9) при
в малорастворимое соединение, потенциалы соответствующих электродов по уравнению Нериста (см. формулы (5.3) и (5.9) при 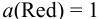 ):
):
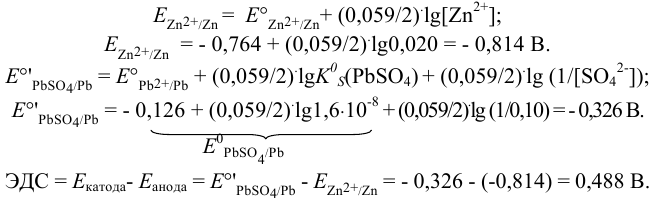
Для протекающей в гальваническом элементе реакции
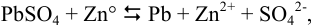
можно вычислить константу равновесия по формуле (5.11):
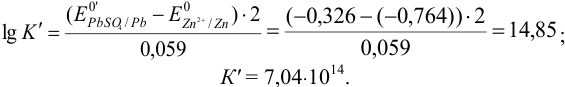
Пример 5.22.
Вычислите ЭДС гальванического элемента:
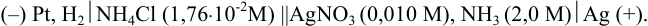
Решение.
Справочные данные: 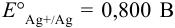 . При вычислениях пренебрежем влиянием ионной силы.
. При вычислениях пренебрежем влиянием ионной силы.
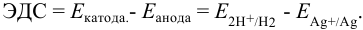
Равновесный потенциал водородного электрода зависит от pH, значение которого при 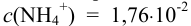 моль/л составляет 5,5 (пример 3.14).
моль/л составляет 5,5 (пример 3.14).
Реакция в анодном полуэлементе: 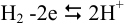 .
.
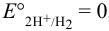 давление водорода — 1 атм. По уравнению Нернста:
давление водорода — 1 атм. По уравнению Нернста:
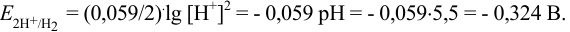
На катоде вместо равновесия 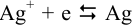 в присутствии избытка
в присутствии избытка  устанавливается равновесие
устанавливается равновесие 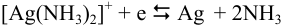 .
.
В таком случае вычисление равновесного потенциала можно провести по формуле (5.7), учитывая, что 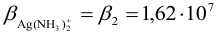 и
и 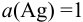 :
:
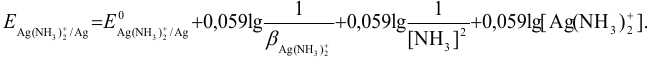
В условиях большого избытка лиганда:
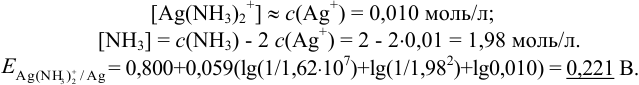
Можно провести расчет равновесного потенциала катода как серебряного электрода, рассчитав 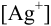 в условиях комплексообразования. В примере 4.1 для указанных условий найдена
в условиях комплексообразования. В примере 4.1 для указанных условий найдена 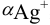 , равная
, равная 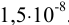 .
.
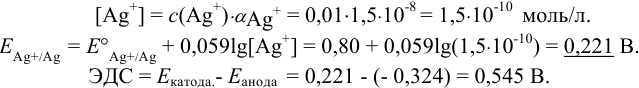
Пример 5.23.*
Вычислите равновесную и аналитическую концентрацию (с учетом ионной силы) ионов свинца в растворе катодного полуэлемента, если после добавления к 20,0 мл раствора соли свинца 1,30 мл 0,0340 М 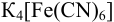 измеренная величина ЭДС гальванического элемента
измеренная величина ЭДС гальванического элемента
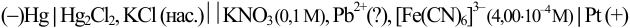
оказалась равной 0,463 В и известно, что добавленное количество 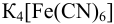 меньше стехиометрического. (Справочные данные приведены в примере 5.12).
меньше стехиометрического. (Справочные данные приведены в примере 5.12).
Решение:
Анодом здесь служит насыщенный каломельный электрод (н.к.э.), потенциал которого равен 0,242 В. Н.к.э. часто используют в электрохимических ячейках как электрод сравнения. Потенциал анода вычислим по величине ЭДС и известному потенциалу катода:
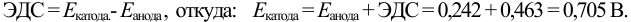
Катодом является инертный электрод 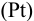 , потенциал которого зависит от активности компонентов редокс- пары
, потенциал которого зависит от активности компонентов редокс- пары 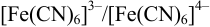 . Ее восстановленная форма, в свою очередь, зависит от активности ионов
. Ее восстановленная форма, в свою очередь, зависит от активности ионов 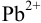 (пример 5,12). Далее решение следует проводить как в примере 5.12 а), где найдено:
(пример 5,12). Далее решение следует проводить как в примере 5.12 а), где найдено:
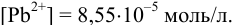
Аналитическая концентрация соли свинца 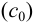 определяется суммой прореагировавшего
определяется суммой прореагировавшего 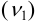 по реакции
по реакции
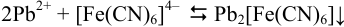
и оставшегося 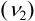 количеств
количеств 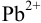 с учетом объемов раствора.
с учетом объемов раствора.
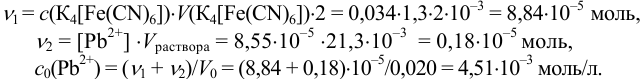
Эти примеры взяты со страницы примеров решения задач по аналитической химии:
Решение задач по аналитической химии
Возможны вам будут полезны эти страницы:

