Интегральный признак задача с решением

Интегральный признак

Теорема. Если функция 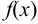, при всех 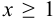, неотрицательна и убывает, то ряд 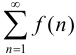сходится тогда и только тогда, когда сходится интеграл .

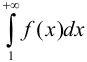Задача №111.

Исследовать на сходимость гармонический ряд .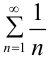

Рассмотрим 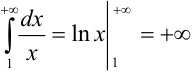. Так как несобственный интеграл расходится, то расходится и гармонический ряд.

Этот материал взят со страницы кратких лекций с решением задач по высшей математике:

Решение задач по высшей математике

Возможно эти страницы вам будут полезны:

Признак Даламбера задача с решением

Признак Коши задача с решением

Знакопеременные и знакочередующиеся ряды. Признак Лейбница задачи с решением

Степенные ряды задачи с решением