Оглавление:
Признак Даламбера
Теорема. Если для ряда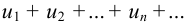 
с положительными членами существует предел 
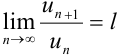, то при 
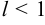ряд сходится, а при 
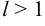— расходится.
Задача №109.
Исследовать сходимость ряда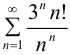 
.
Решение:
Воспользуемся признаком Даламбера:
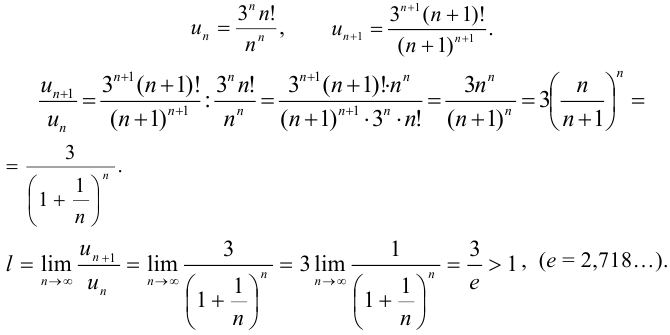
Так как 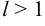, то ряд расходится.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Первый признак сравнения рядов задачи с решением |
| Предельная форма признака сравнения задача с решением |
| Признак Коши задача с решением |
| Интегральный признак задача с решением |
