Оглавление:
Методы вычисления определённых интегралов
Замена переменной
Теорема. Пусть функция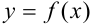 
непрерывна на 
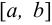. Отрезок 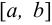является множеством значений функции 
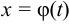, определенной на 
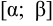и имеющей на нем непрерывную производную, причем 
, 
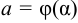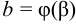. Тогда имеет место формула:
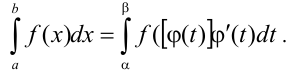
В интеграле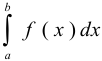 
сделаем замену переменных при помощи подстановки 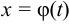или 
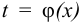. При этом необходимо перейти от старых пределов интегрирования 
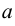и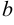 
к новым 
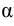и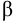 
, которые определяются из уравнений , .
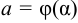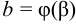Задача №93.
Вычислить интеграл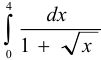 
.
Решение:
Перейдём к новой переменной интегрирования, полагая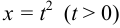 
. При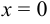 
получаем 
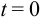, при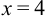 
имеем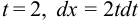 
.
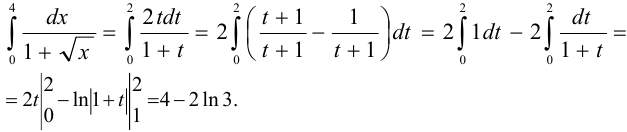
Интегрирование по частям
Теорема. Пусть функци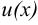и 
и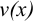 
имеют на 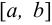непрерывные производные. Тогда справедливо равенство
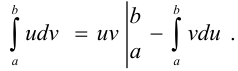
Задача №94.
Найти интеграл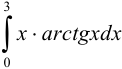 
.
Решение:
Положим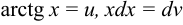 
, тогда 
, 
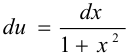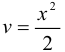. Имеем
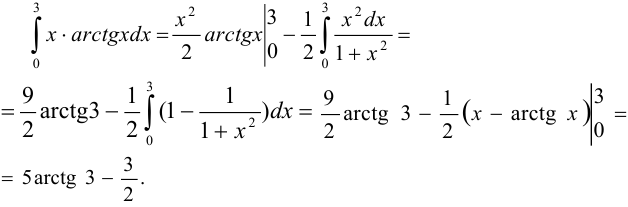
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
