Оглавление:
Интегрирование некоторых видов иррациональностей
1. Рассмотрим интеграл вида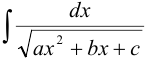 
. Чтобы его проинтегрировать необходимо уметь находить интегралы 
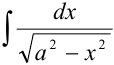и 
.
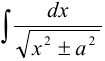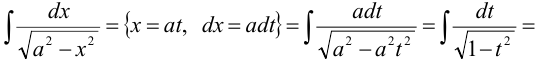
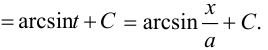
Второй интеграл приведем к табличному заменой переменной: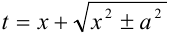 
(подстановка Эйлера). Тогда 
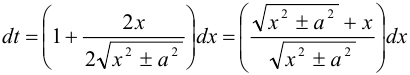или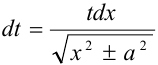 
. Откуда 
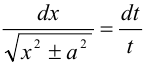. Таким образом,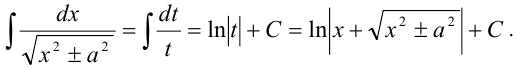 
Задача №89.
Вычислить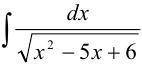 
.
Выделим в подкоренном выражении полный квадрат:
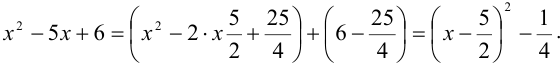
Произведем замену: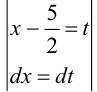 
, тогда
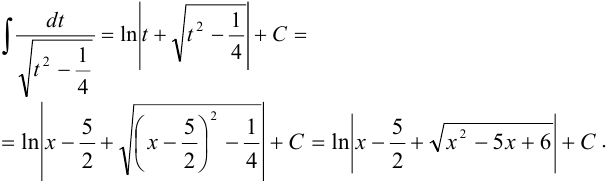
2. Рассмотрим интеграл вида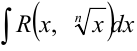 
, где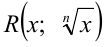 
— рациональная функция от 
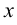и 
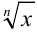, а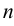 
— натуральное число. С помощью замены переменной 
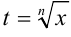нахождение такого интеграла сводится к нахождению интеграла от дробно-рациональной функции относительно 
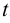. Если в подынтегральную функцию входят радикалы с разными показателями, то за 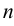следует взять их наименьшее общее кратное.
Задача №90.
Вычислить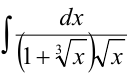 
.
Общее наименьшее кратное 2 и 3 есть 6. Значит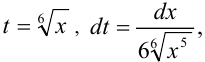 
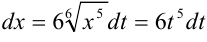. Отсюда
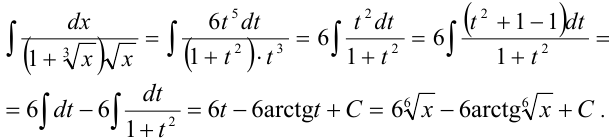
3. Рассмотрим интеграл от рациональной функции вида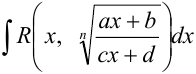 
, где 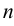— натуральное число. Этот интеграл с помощью замены переменной 
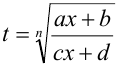сводится к интегралу от дробно-рациональной функции.
Задача №91.
Вычислить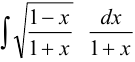 
.
Положим
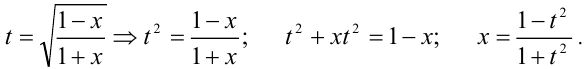
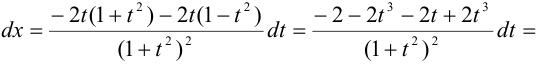
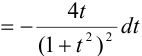
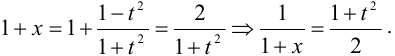
Таким образом,
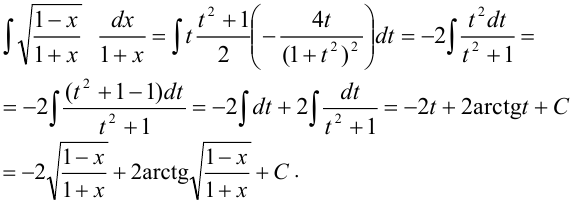
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
