Оглавление:
Интегрирование рациональных дробей
Интегрирование рациональных дробей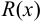 
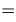
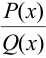— где 
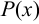и
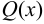— многочлены с действительными коэффициентами, выполняется в три шага:
1) если дробь неправильная, т. е. степень числителя больше или равна степени знаменателя, то выделяют целую часть рациональной дроби 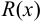, деля 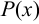на 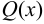по правилу деления многочлена на многочлен. После этого рациональная дробь может быть записана в виде суммы выделенной целой части — многочлена 
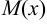и правильной остаточной дроби 
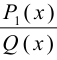, т. е. 
;
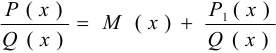2) правильную остаточную дробь 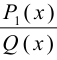разлагают на простейшие дроби. Для этого находят корни уравнения 
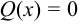и разлагают знаменатель 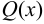на множители первой и второй степени с действительными коэффициентами:
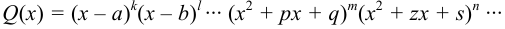
В этом разложении знаменателя 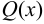множители первой степени соответствуют действительным корням, а множители второй степени — парам мнимых сопряжённых корней. Коэффициент при наибольшей степени 
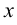в знаменателе 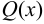можно считать равным 1, ибо этого всегда можно добиться, деля на него 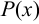и 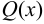. После этого правильная остаточная дробь разлагается на простейшие по формуле:
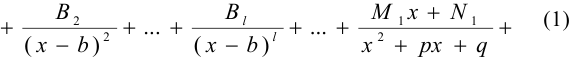
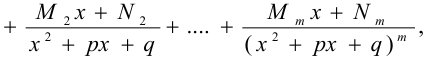
где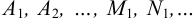 
— неизвестные коэффициенты. Для нахождения неопределённых коэффициентов все простейшие дроби приводят к общему знаменателю 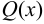и приравнивают числители обеих частей равенства (1). Затем сравнивают коэффициенты при одинаковых степенях 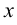. Это приводит к системе уравнений, из которой и находятся значения коэффициентов;
3) дальше находят интегралы выделенной целой части и всех простейших дробей, которые затем складывают.
Задача №83.
Найти интеграл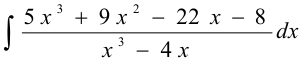 
.
Решение:
Подынтегральная рациональная дробь неправильная. Выделим целую часть. Для этого разделим числитель на знаменатель:
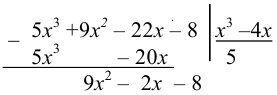
Таким образом,
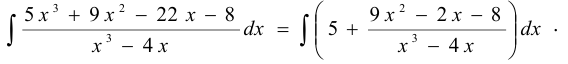
Знаменатель правильной остаточной дроби разложим на множители:
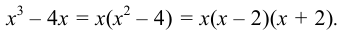
Разложим остаточный член на простейшие по формуле (1):
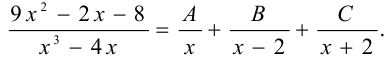
Приведём правую часть к общему знаменателю и приравняем числители:
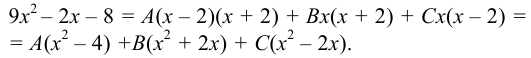
Коэффициенты при одинаковых степенях 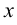в обеих частях тождества должны быть равны, поэтому получим систему уравнений
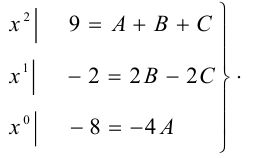
Имеем: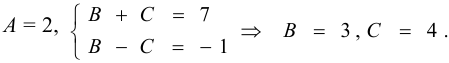 
Метод, которым найдены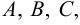 
называется способом сравнения коэффициентов.
Для определения коэффициентов часто бывает удобнее применять способ частных значений, состоящий в том, что аргументу 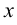придают некоторые удобные значения (чаще значения корней):
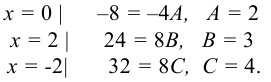
Вычислим данный интеграл
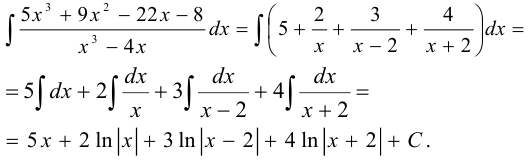
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
