Интегрирование по частям задача с решением

Интегрирование по частям

Если функци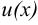и и 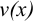дифференцируемы на множестве 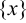и на этом множестве существует интеграл 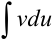, тогда

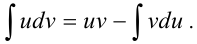
Для интегралов 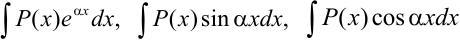за 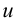следует принять 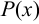, а за 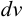— соответственно выражения .

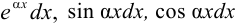Для интегралов вид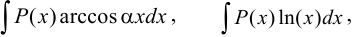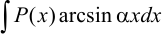а за 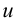принимаются, соответственно, функции ,
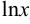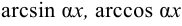, а за 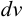— выражение .

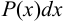Задача №79.

Вычислить интеграл .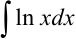

Решение:

Воспользуемся формулой .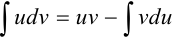

Положим 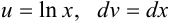, тогда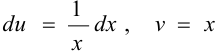

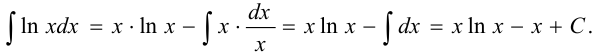
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:

Решение задач по высшей математике

Возможно эти страницы вам будут полезны:

Неопределённые интегралы задачи с решением

Интегрирование заменой переменной (подстановкой) задачи с решением

Интегрирование простейших рациональных дробей задачи с решением

Интегрирование рациональных дробей задача с решением