Оглавление:
Полный дифференциал
Произведение частной производной на приращение соответствующей независимой переменной называется частным дифференциалом:
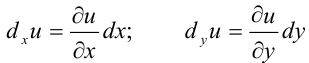и т. д.
Сумма частных дифференциалов по всем независимым переменным называется полный дифференциал:
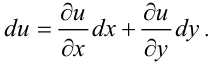
Задача №69.
Найти полный дифференциал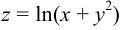 
.
Решение:
.
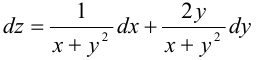Функция, имеющая полный дифференциал в каждой точке некоторой области, называется дифференцируемой в этой области.
Из дифференцируемости функции в некоторой области следует ее непрерывность в этой области, но не наоборот.
Теорема. Если функция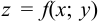 
имеет непрерывные частные производные 
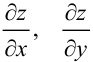в некоторой области, то она дифференцируема в этой области.
Как и в случае функции одной переменной полный дифференциал является главной линейной частью относительно приращений независимых переменных полного приращения функции.
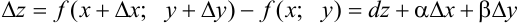, где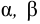 
-бесконечно малые величины при 
.
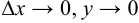Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Функция двух переменных задача с решением |
| Частная производная задача с решением |
| Частные производные высших порядков в высшей математике |
| Экстремум функции нескольких переменных задачи с решением |
