Асимптоты графика функции
Если расстояние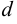 
от точки кривой 
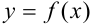, имеющей бесконечную ветвь, до некоторой определённой прямой по мере удаления точки до этой кривой в бесконечность стремится к 0, то прямая называется асимптотой кривой.
Различают асимптоты: горизонтальные, вертикальные, наклонные.
1. Кривая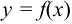 
имеет горизонтальную асимптоту 
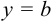только в том случае, когда существует конечный предел функции при 
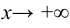или при 
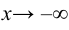, и этот предел равен 
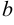, т. е. если 
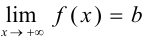или 
.
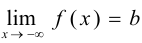2. Кривая 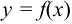имеет вертикальную асимптоту 
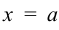, если при 
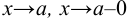или при 
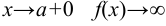. Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых 
неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются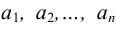 
, то уравнения вертикальных асимптот будут 
.
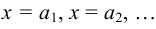3. Для определения наклонной асимптоты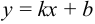 
кривой 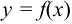надо найт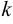и 
и 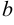из формул
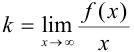и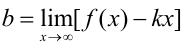 
(следует отдельно рассматривать случаи 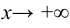, ). Наклонные асимптоты у кривой 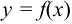существуют только в том случае, когда пределы 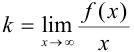и 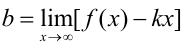имеют конечное значение. Если окажется, что 
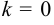, a 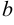имеет конечное значение, то асимптота будет горизонтальной. При определении этих пределов удобно пользоваться правилом Лопиталя.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
