Правило для исследования функции на экстремум первым способом
Для исследования функции па экстремум по первой производной следует:
- Найти
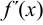. - Решить уравнение
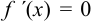, а также определить те значения 
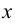, при которых 
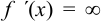и не существует (найти критические точки функции). Пусть ими будут точки 
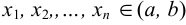. - Все критические точки расположить в порядке возрастания их абсцисс в интервале
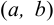
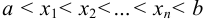. - Внутри каждого интервала
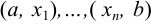взять любую точку и установить в этой точке знак 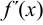. - Рассмотреть знаки 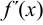в двух соседних интервалах, переходя последовательно слева направо от первого интервала к последнему. Если при таком переходе знаки 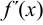в двух соседних интервалах различны, то экстремум в критической точке есть. Максимум будет, если знак поменяется с « + » на « — », а минимум будет, если знак поменяется с « — »на « + ». Если же в двух соседних интервалах имеет место сохранение знака первой производной, то экстремума в рассматриваемой критической точке нет.
- Найти значение функции в точках, где она достигает экстремума (экстремальное значение функции).
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
