Первое достаточное условие существования экстремума функции
Теорема. Пусть точка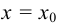 
является критической точкой функции 
, а сама функция непрерывна и дифференцируема во всех точках некоторого интервала, содержащего эту точку. Тогда:
- Если при
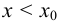
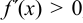, а при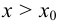 
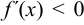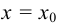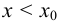
, то при имеет место максимум, т. е. если при переходе слева па право через критическую точку первая производная функции меняет знак с « + » на «- », то в этой точке функция достигает максимума. - Если при 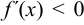, а при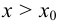 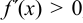, то при 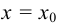имеет место минимум, иначе если при переходе слева па право через критическую точку
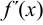меняет знак с «- » на « + », то в этой точке функция достигает минимума. - Если при переходе через критическую точку 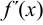не меняет знак, то экстремума нет.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
