Дифференцируемая функция. Применение дифференциала в приближенных вычислениях
Из определения производной имеем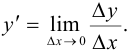 
По определению предела функции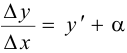 
, где 
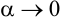, при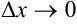 
. Отсюда 
.
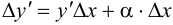При малых значениях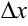 
и при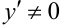 
, имеем 
.
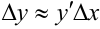Главная часть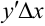 
приращения 
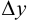функции, линейной относительно 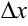, называется дифференциалом функции и обозначается 
.
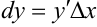Положив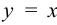 
, получим 
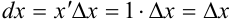и поэтому 
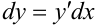или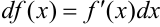 
.
Дифференциалом функции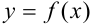 
называется произведение производной этой функции на приращение независимой переменной.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
