Оглавление:
Кривые линии второго порядка
Общее уравнение кривых второго порядка имеет вид: 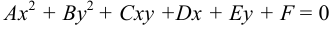 ,
,
где 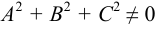 .
.
К кривым линиям второго порядка относятся: окружность, эллипс, гипербола и парабола.
Окружность
Окружностью называется множество точек плоскости, равноудаленных от одной и той же точки — центра окружности.
Утверждение. Окружность является кривой второго порядка и ее каноническое уравнение имеет вид:
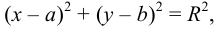
где 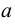 и
и 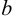 — координаты центра окружности;
— координаты центра окружности; 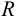 — радиус окружности.
— радиус окружности.
Доказательство. Рассмотрим окружность с заданными параметрами в системе координат на плоскости. Возьмем произвольную точку этой окружности 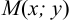 .
.
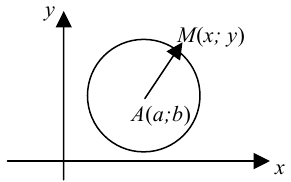
По формуле расстояния между двумя точками имеем:
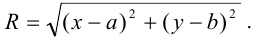
Возведем обе части уравнения в квадрат и получим
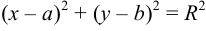 — уравнение окружности.
— уравнение окружности.
Задача №24.
Показать, что уравнение 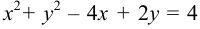 является окружностью. Найти ее центр и радиус.
является окружностью. Найти ее центр и радиус.
Решение:
Заданное уравнение приведем к виду 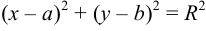 .
.
Сгруппируем члены, содержащие только 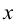 и только
и только 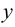 следующим образом:
следующим образом:
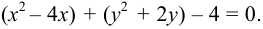
Допишем теперь до квадрата разности и суммы:
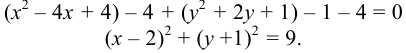
Кривая является окружностью с центром 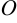 (2; -1) и радиусом
(2; -1) и радиусом 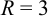 .
.
Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная равная 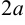 .
.
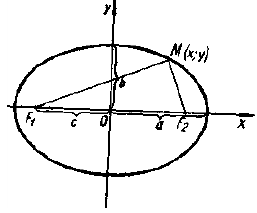
Утверждение. Эллипс является кривой второго порядка, и каноническое уравнение эллипса имеет вид:
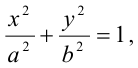
где 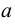 и
и 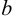 — полуоси эллипса.
— полуоси эллипса.
Доказательство. Пусть 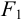 и
и 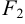 — некоторые фиксированные точки плоскости, являющиеся фокусами эллипса и пусть точка
— некоторые фиксированные точки плоскости, являющиеся фокусами эллипса и пусть точка 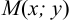 — произвольная точка данного эллипса. Расположим систему координат так, чтобы ось
— произвольная точка данного эллипса. Расположим систему координат так, чтобы ось 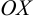 проходила через точки
проходила через точки 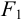 и
и 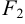 , а начало координат делило бы отрезок
, а начало координат делило бы отрезок 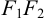 пополам.
пополам.
Предположим, что расстояние между фокусами равно 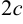 , тогда
, тогда 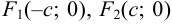 и пусть
и пусть 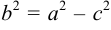 . Из определения эллипса имеем
. Из определения эллипса имеем 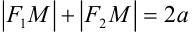 . Но по формуле расстояния между двумя точками
. Но по формуле расстояния между двумя точками
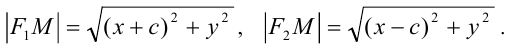
Получаем:
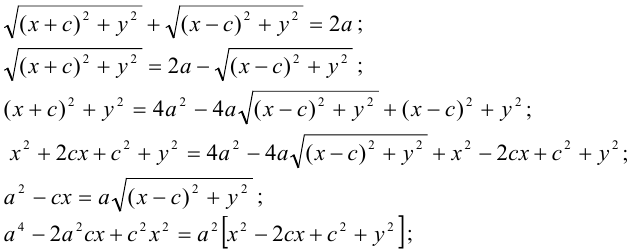
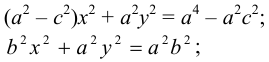
или
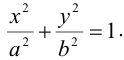
Если 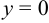 , то
, то 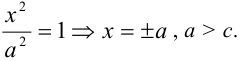
Если 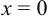 , то
, то 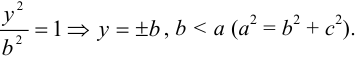
Число 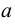 называется большой полуосью эллипса, число
называется большой полуосью эллипса, число 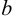 — малой полуосью эллипса,
— малой полуосью эллипса, 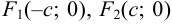 — фокусы. Между
— фокусы. Между 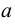 ,
, 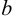 и
и 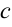 существует соотношение
существует соотношение 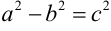 .
.
Эксцентриситетом эллипса называется отношение 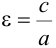 . Ясно, что
. Ясно, что 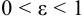 . Если
. Если 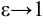 , то форма эллипса будет стремиться к форме отрезка
, то форма эллипса будет стремиться к форме отрезка 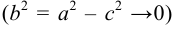 . Если
. Если 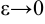 , то форма эллипса будет стремиться к форме окружности.
, то форма эллипса будет стремиться к форме окружности.
Если 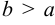 , то эллипс вытянут вдоль оси
, то эллипс вытянут вдоль оси 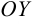 , большой полуосью будет
, большой полуосью будет 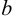 , а малой —
, а малой — 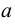 , фокусы лежат на оси
, фокусы лежат на оси 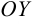 и
и 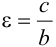 .
.
Задача №25.
Найти координаты фокусов эллипса и его эксцентриситет, если известно уравнение эллипса:
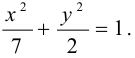
Решение:
Уравнение имеет канонический вид и 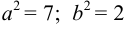 .
.
Найдем 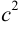 .
. 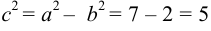 или
или 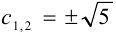 , значит
, значит
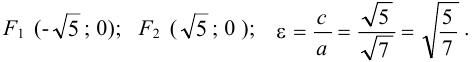
Задача №26.
Показать, что уравнение 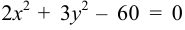 является уравнением эллипса. Найти оси, фокусы и эксцентриситет этого эллипса.
является уравнением эллипса. Найти оси, фокусы и эксцентриситет этого эллипса.
Решение:
Приведем уравнение к каноническому виду:
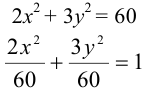
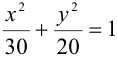 — каноническое уравнение данного эллипса.
— каноническое уравнение данного эллипса.
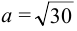 — большая полуось;
— большая полуось; 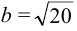 — малая полуось. Найдем координаты фокусов. Так как
— малая полуось. Найдем координаты фокусов. Так как 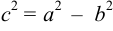 , то
, то
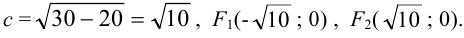
Эксцентриситет 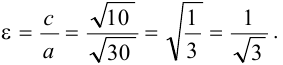
Гипербола
Гиперболой называется множество точек плоскости, абсолютное значение разности расстояний которых от двух точек, называемых фокусами, есть величина постоянная.
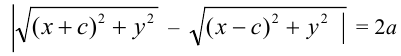
или
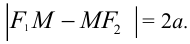
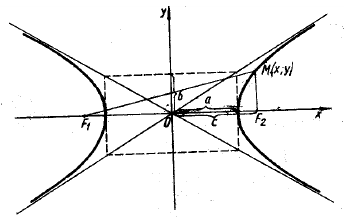
Утверждение. Гипербола является кривой второго порядка, и ее каноническое уравнение имеет вид: 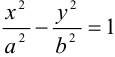 . Число
. Число 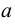 называется действительной полуосью, число
называется действительной полуосью, число 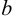 называется мнимой полуосью и
называется мнимой полуосью и 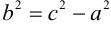 .
.
Доказательство. Пусть 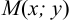 — произвольная точка гиперболы. Пусть
— произвольная точка гиперболы. Пусть 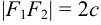 и
и 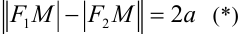 . Очевидно, что
. Очевидно, что 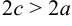 . По формуле расстояний между двумя точками получим:
. По формуле расстояний между двумя точками получим:
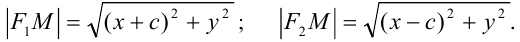
Положим 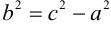 . Подставим предыдущие равенства в (*).
. Подставим предыдущие равенства в (*).
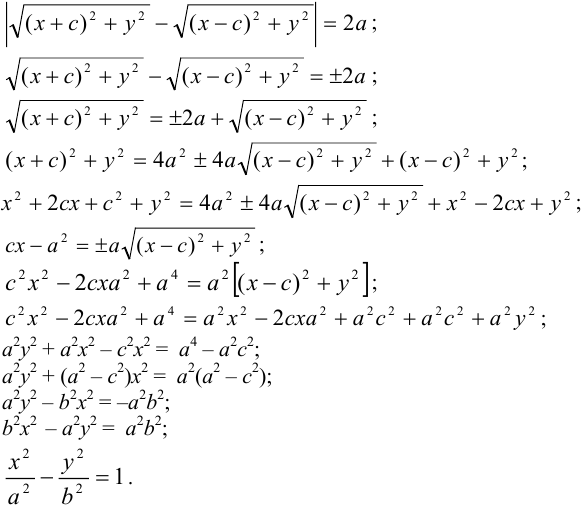
Если 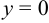 , то
, то 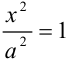 и
и 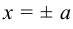 — точки пересечения гиперболы с осью
— точки пересечения гиперболы с осью 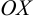 . Очевидно, что точек пересечения с осью
. Очевидно, что точек пересечения с осью 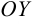 нет.
нет.
Эксцентриситетом гиперболы называют отношение 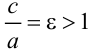 . Эта величина характеризует форму гиперболы. Гипербола имеет две асимптоты
. Эта величина характеризует форму гиперболы. Гипербола имеет две асимптоты 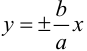 .
.
Задача №27.
Составить каноническое уравнение гиперболы, если 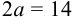 .
.
Решение:
Так как 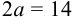 , то
, то 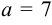 .
. 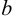 можем найти из соотношения
можем найти из соотношения 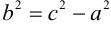 . Для этого найдем
. Для этого найдем 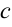 из равенства
из равенства 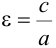 .
.
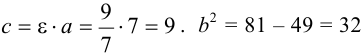 , значит
, значит 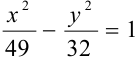 — уравнение данной гиперболы.
— уравнение данной гиперболы.
Задача №28.
Показать, что уравнение 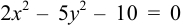 является уравнением гиперболы. Найти оси, фокусы, эксцентриситет и уравнения асимптот.
является уравнением гиперболы. Найти оси, фокусы, эксцентриситет и уравнения асимптот.
Решение:
Приведем уравнение к каноническому виду:
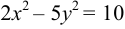 или
или 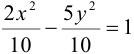 .
.
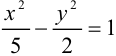 — каноническое уравнение данной гиперболы.
— каноническое уравнение данной гиперболы.
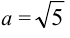 — действительная полуось;
— действительная полуось; 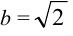 — мнимая полуось.
— мнимая полуось.
Найдем координаты фокуса. 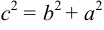 или
или  .
.
Значит 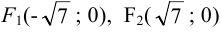 — фокусы гиперболы.
— фокусы гиперболы.
Эксцентриситет 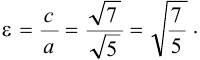
Асимптоты имеют следующие уравнения: 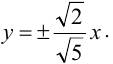
Парабола
Параболой называется множество точек плоскости, каждая из которой одинаково удалена от данной точки 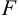 , называемой фокусом, и от данной прямой, не проходящей через данную точку и называемой директрисой.
, называемой фокусом, и от данной прямой, не проходящей через данную точку и называемой директрисой.
Утверждение. Парабола является кривой второго порядка и ее каноническое уравнение имеет вид: 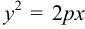 , где
, где 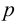 — расстояние от фокуса до директрисы.
— расстояние от фокуса до директрисы.
Доказательство. Построим систему координат так, чтобы ось 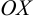 проходила через точку
проходила через точку 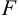 перпендикулярно директрисе
перпендикулярно директрисе 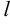 , а начало координат делило расстояние от фокуса до директрисы пополам.
, а начало координат делило расстояние от фокуса до директрисы пополам.
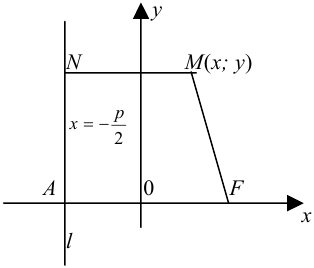
Предположим расстояние 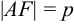 , тогда точка
, тогда точка 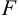 имеет координаты
имеет координаты 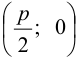 , а уравнение директрисы
, а уравнение директрисы 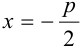 . Пусть точка
. Пусть точка 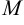 принадлежит параболе, а точка
принадлежит параболе, а точка 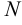 — ее проекция на директрису, тогда по определению расстояние
— ее проекция на директрису, тогда по определению расстояние 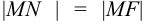 . Но
. Но 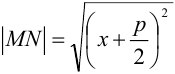 и
и 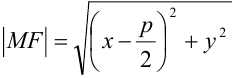 . Таким образом,
. Таким образом,
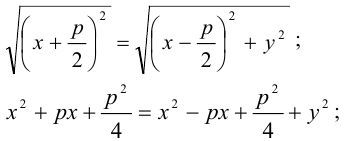
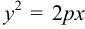 — каноническое уравнение параболы.
— каноническое уравнение параболы.
Если 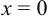 , то
, то 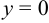 , таким образом, парабола проходит через начало координат. Функция симметрична относительно оси
, таким образом, парабола проходит через начало координат. Функция симметрична относительно оси 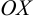 .
.
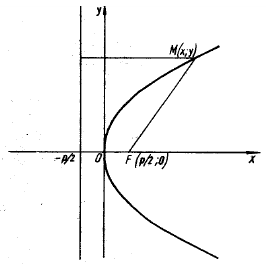
Если 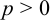 , то ветви параболы направлены вправо, если
, то ветви параболы направлены вправо, если 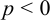 , то — влево.
, то — влево.
Задача №29.
Найти координаты фокуса и уравнение директрисы следующей параболы 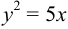 .
.
Решение:
Запишем уравнение следующим образом:
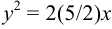 , следовательно,
, следовательно, 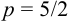 .
.
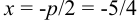 — уравнение директрисы.
— уравнение директрисы.
Координаты фокуса: 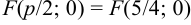 .
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

