Оглавление:
Скалярное, векторное и смешанное произведения векторов
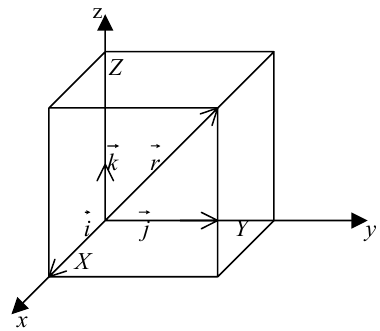
Пусть задана декартова прямоугольная система координат в пространстве. Введем в рассмотрение единичные векторы 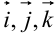 координатных осей. Тогда всякий вектор
координатных осей. Тогда всякий вектор 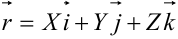 , где
, где 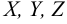 — проекции вектора
— проекции вектора 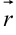 на соответствующие координатные оси. На основании теоремы о диагонали прямоугольного параллелепипеда заключаем:
на соответствующие координатные оси. На основании теоремы о диагонали прямоугольного параллелепипеда заключаем: 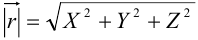 — длина вектора.
— длина вектора.
Скалярное произведение
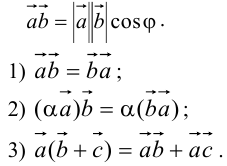
Доказательство следует из определения скалярного произведения.
Теорема. Скалярное произведение двух векторов 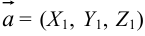 и
и 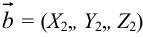 выражается формулой:
выражается формулой: 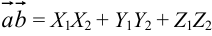 .
.
Доказательство. Из определения скалярного произведения двух векторов имеем:
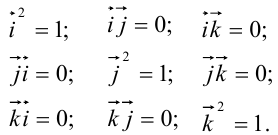
По условию теоремы имеем:
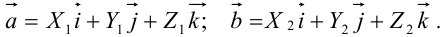
Тогда по свойству 3):
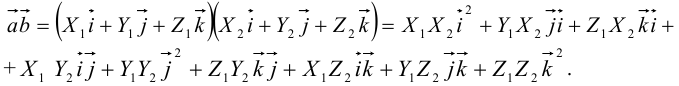
Из таблицы, приведенной вначале теоремы, заключаем:
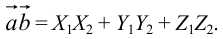
Следствие 1. Косинус угла между двумя векторами определяется формулой
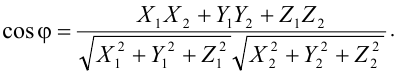
Следствие 2. Два вектора 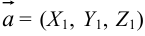 и
и 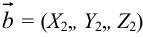 взаимно перпендикулярны тогда и только тогда, если
взаимно перпендикулярны тогда и только тогда, если 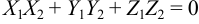 .
.
Пусть имеется тройка упорядоченных векторов  ,
, 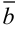 ,
, 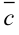 , которые некомпланарны и приложены в одной точке. Будем смотреть с конца вектора
, которые некомпланарны и приложены в одной точке. Будем смотреть с конца вектора 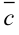 на векторы
на векторы  и
и 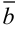 . Если кратчайший поворот от вектора
. Если кратчайший поворот от вектора  к вектору
к вектору 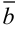 совершается против часовой стрелки, то тройка называется правой, если — по часовой стрелке, то тройка называется левой. Будем пользоваться правыми декартовыми системами координат
совершается против часовой стрелки, то тройка называется правой, если — по часовой стрелке, то тройка называется левой. Будем пользоваться правыми декартовыми системами координат 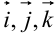 .
.
Векторное произведение двух векторов
Векторным произведением двух векторов  и
и 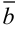 называется вектор
называется вектор 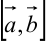 , который удовлетворяет следующим свойствам:
, который удовлетворяет следующим свойствам:
1) 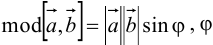 — угол между векторами
— угол между векторами  и
и 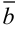 ;
;
2) вектор 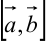 перпендикулярен каждому из векторов
перпендикулярен каждому из векторов  и
и 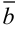 ;
;
3) тройки ( ,
, 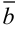 ,
, 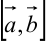 ) и (
) и (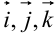 ) являются тройками одной ориентации.
) являются тройками одной ориентации.
Свойства векторного произведения двух векторов:
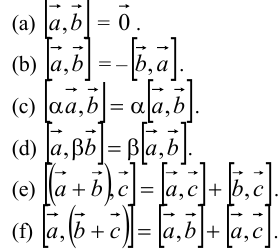
Доказательство следует из определения векторного произведения.
Теорема. Векторное произведение двух векторов 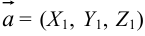 ;
; 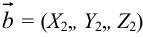 выражается формулой:
выражается формулой:
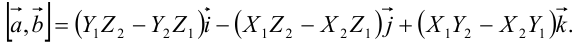
Формула в теореме символически записывается следующим образом:
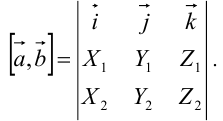
Следствие 3. Площадь параллелограмма, построенного на векторах 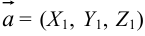 и
и 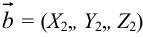 , вычисляется по формуле
, вычисляется по формуле
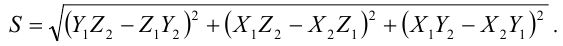
Следствие 4. Площадь треугольника 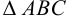 определяется формулой
определяется формулой
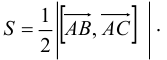
Задача №22.
Вычислить площадь 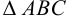 , если
, если 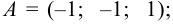

Решение:
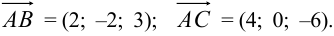
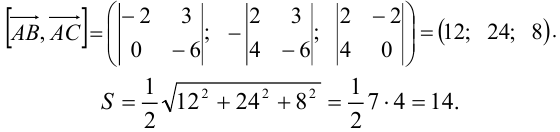
Смешанное произведение трех векторов
Пусть даны три вектора 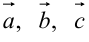 . Их смешенным произведением
. Их смешенным произведением
называется число 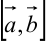
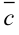 .
.
Теорема. Смешанное произведение трех некомпланарных векторов равно объему параллелепипеда, построенного на векторах 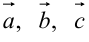 , взятому со знаком плюс, если тройка
, взятому со знаком плюс, если тройка 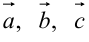 — правая, и со знаком минус, если эта тройка — левая.
— правая, и со знаком минус, если эта тройка — левая.
Теорема. Смешанное произведение трех векторов: 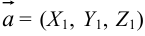 ,
, 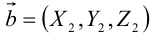 ,
, 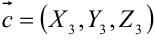 определяется по формуле
определяется по формуле
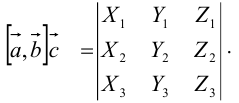
Задача №23.
Даны векторы 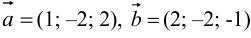 . Найти их скалярное, векторное произведения и угол между ними.
. Найти их скалярное, векторное произведения и угол между ними.
Решение:
Скалярное произведение 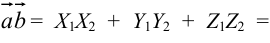
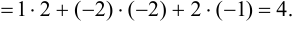
Векторное произведение векторов :
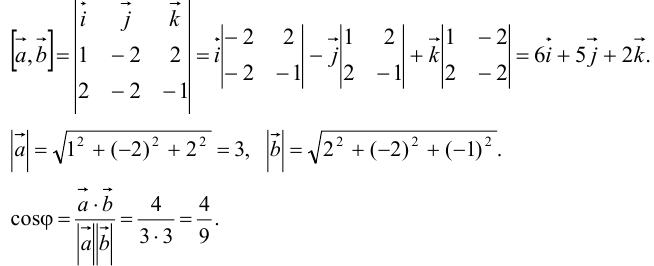
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Векторы и операции над ними задачи с решением |
| Плоскость и прямая в пространстве задача с решением |
| Кривые линии второго порядка задачи с решением |
| Числовые последовательности задачи с решением |

