Оглавление:
Прямая на плоскости
Уравнением линии на плоскости называется такое уравнение вида 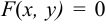 , которому удовлетворяют координаты любой точки этой линии.
, которому удовлетворяют координаты любой точки этой линии.
Прямую линию на плоскости относительно системы декартовых прямоугольных координат можно задать различными способами. В зависимости от способа задания прямой рассматривают различные виды ее уравнения.
Углом между прямой и положительным направлением оси называют угол, который отсчитывается от оси 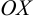 к прямой против часовой стрелки.
к прямой против часовой стрелки.
1. Уравнение прямой с угловым коэффициентом
Пусть прямая задана на плоскости двумя параметрами: углом наклона, т. е. углом, который образует эта прямая с положительным направлением оси 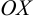 и числом
и числом 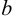 , равным расстоянию между точкой пересечения этой прямой с осью
, равным расстоянию между точкой пересечения этой прямой с осью 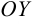 и началом координат. Требуется написать уравнение этой прямой. Пусть
и началом координат. Требуется написать уравнение этой прямой. Пусть 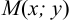 — произвольная точка, взятая на этой прямой.
— произвольная точка, взятая на этой прямой.
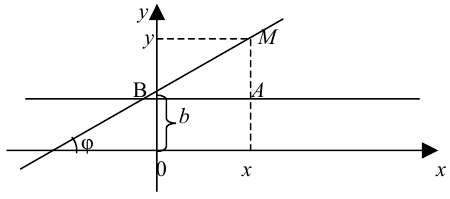
Рассмотрим 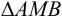 . Ясно, что
. Ясно, что 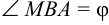 . Имеем
. Имеем

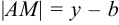 ,
, 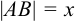 . Обозначим:
. Обозначим: 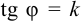 — угловой коэффициент данной прямой. Подставляя три последние равенства в (*), получим:
— угловой коэффициент данной прямой. Подставляя три последние равенства в (*), получим:
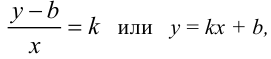
где 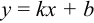 — уравнение прямой с данным угловым коэффициентом
— уравнение прямой с данным угловым коэффициентом 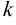 ;
; 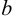 — величина отрезка, отсекаемого прямой на оси ординат
— величина отрезка, отсекаемого прямой на оси ординат 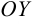 . При
. При 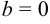 ,
, 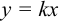 — прямая, проходящая через начало координат.
— прямая, проходящая через начало координат.
2. Общее уравнение прямой 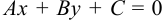 ,
, 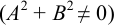 :
:
а) если 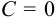 , то
, то 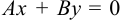 . Прямая проходит через начало координат, т. е.
. Прямая проходит через начало координат, т. е. 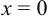 ,
, 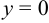 ;
;
б) если 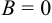 ,
, 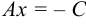 ,
, 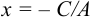 . Прямая параллельна оси
. Прямая параллельна оси 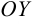 ;
;
в) если 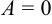 , то
, то 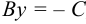 ,
, 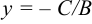 . Прямая параллельна оси
. Прямая параллельна оси 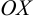 ;
;
г) 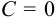 и
и 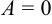 ,
, 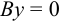 или
или 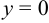 . Это уравнение оси
. Это уравнение оси 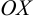 ;
;
д) 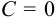 и
и 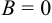 ,
, 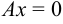 или
или 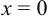 . Это уравнение оси
. Это уравнение оси 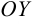 .
.
3. Уравнение прямой в отрезках на осях 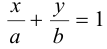 .
.
Общее уравнение прямой 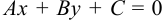 преобразуем следующим образом:
преобразуем следующим образом: 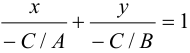 . Обозначим:
. Обозначим: 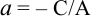 — величина отрезка, отсекаемого прямой на оси
— величина отрезка, отсекаемого прямой на оси 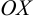 ;
; 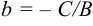 — величина отрезка, отсекаемого прямой на оси
— величина отрезка, отсекаемого прямой на оси 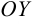 .
.
4. Уравнение пучка прямых 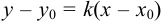 .
.
Пучком прямых на плоскости называется множество всех прямых, проходящих через данную точку.
Пусть в системе координат на плоскости дана точка 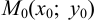 . Проведем через эту точку произвольную прямую и напишем ее уравнение. Пусть
. Проведем через эту точку произвольную прямую и напишем ее уравнение. Пусть 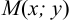 — произвольная точка на прямой, а
— произвольная точка на прямой, а 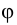 —угол наклона. Так как
—угол наклона. Так как 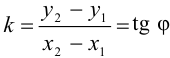 , то
, то 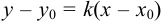 — уравнение пучка прямых, проходящих через точку
— уравнение пучка прямых, проходящих через точку 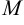
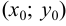 .
.
5. Уравнение прямой, проходящей через две точки
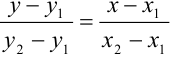
Пусть даны две различные точки 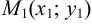 и
и 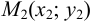 . Через эти точки проходит единственная прямая. Угловой коэффициент прямой, проходящей через две заданные точки, определяется формулой
. Через эти точки проходит единственная прямая. Угловой коэффициент прямой, проходящей через две заданные точки, определяется формулой 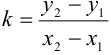 . Прямая проходит через точку
. Прямая проходит через точку 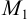 значит уравнение пучка прямых будет:
значит уравнение пучка прямых будет: 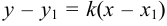 или
или 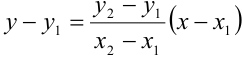 . Отсюда
. Отсюда 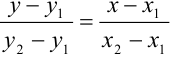 — уравнение прямой, проходящей через две точки.
— уравнение прямой, проходящей через две точки.
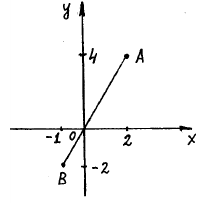
Задача №15.
Даны две точки  (2; 4),
(2; 4), 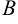 (-1; -2). Написать уравнение прямой, проходящей через
(-1; -2). Написать уравнение прямой, проходящей через  и
и 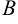 , сделать чертеж.
, сделать чертеж.
Решение:
Уравнение прямой, проходящей через две точки, имеет вид:
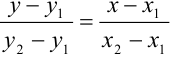 .
.
Подставим координаты точек  и
и 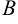 в данное уравнение:
в данное уравнение:
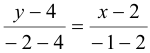 или
или 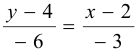 ,
,
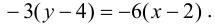
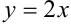 — уравнение прямой, проходящей через точки
— уравнение прямой, проходящей через точки  и
и 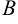 . В этом уравнении
. В этом уравнении 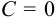 , значит прямая проходит через начало координат.
, значит прямая проходит через начало координат.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

