Оглавление:
Метод последовательного исключения неизвестных (метод Гаусса)
Решение системы линейных уравнений методом Гаусса осуществляется по следующей схеме.
1. Выбираем одно из уравнений системы, в котором коэффициент при одном из неизвестных, например, при 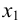 , отличен от нуля. Производя над уравнениями системы преобразования, которые приводят к равносильной системе, исключаем неизвестное из всех уравнений, кроме выбранного ранее. В этом заключается первый шаг метода Гаусса.
, отличен от нуля. Производя над уравнениями системы преобразования, которые приводят к равносильной системе, исключаем неизвестное из всех уравнений, кроме выбранного ранее. В этом заключается первый шаг метода Гаусса.
В результате первого шага может получиться такая система, о которой можно сразу сказать, что она несовместна, а следовательно, и данная система также несовместна.
Если полученная система состоит только из одного выбранного нами уравнения, то исходная система имеет одно решение или бесчисленное множество решений в зависимости от того, имеются ли свободные неизвестные. Во всех остальных случаях переходим ко второму шагу.
2. В системе, полученной в результате первого шага, выбираем одно из уравнений (отличное от выбранного в первом шаге), в котором коэффициент при другом неизвестном, например, при 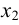 , отличен от нуля. Исключаем
, отличен от нуля. Исключаем 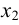 из всех уравнений, кроме двух выбранных.
из всех уравнений, кроме двух выбранных.
Если это нужно, аналогично производим последующие шаги.
После нескольких шагов будет иметь место один из случаев:
а) получится явно несовместная система;
б) получится треугольная система, т. е. система вида
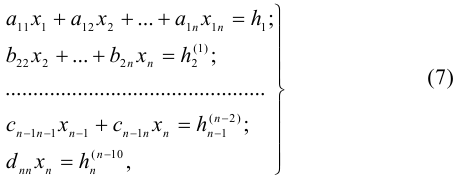
где 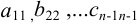 ,
, 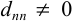 .
.
Система (7), а следовательно, и исходная система имеет единственное решение. Так как 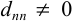 , то из последнего уравнения (7) находим
, то из последнего уравнения (7) находим 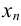 . В предпоследнее уравнение подставляем
. В предпоследнее уравнение подставляем 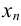 , получим единственное значение для
, получим единственное значение для 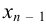 , так как
, так как 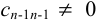 . Продолжая этот процесс, находим последовательно
. Продолжая этот процесс, находим последовательно 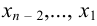 . Указанный способ нахождения неизвестных называется обратным ходом метода Гаусса;
. Указанный способ нахождения неизвестных называется обратным ходом метода Гаусса;
в) получится трапециевидная система, т. е. система вида:
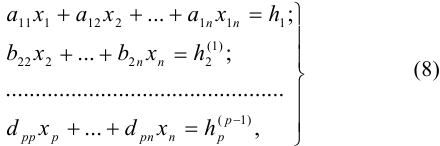
где 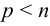 ,
, 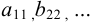 ,
, 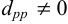 .
.
В системе (8) число неизвестных больше числа уравнений. Так как 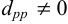 , то из последнего уравнения этой системы
, то из последнего уравнения этой системы 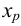 единственным образом выражается через
единственным образом выражается через 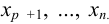 . Осуществляя обратный ход, выразим единственным образом неизвестные
. Осуществляя обратный ход, выразим единственным образом неизвестные 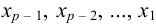 через
через 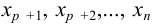 . Придавая последним произвольные значения
. Придавая последним произвольные значения 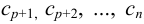 , получим бесконечно много решений системы (8), а следовательно, и данной системы.
, получим бесконечно много решений системы (8), а следовательно, и данной системы.
Заметим, что при применении метода Гаусса на практике имеет смысл вместо преобразований системы производить соответствующие преобразования над строками расширенной матрицы системы, т. е. приводить расширенную матрицу системы к трапециевидной с помощью элементарных преобразований над строками.
Задача №11.
Решить методом Гаусса систему
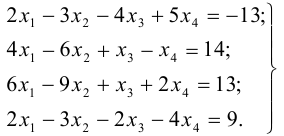
Решение:
Расширенная матрица системы имеет вид

Прибавив ко второй строке первую, умноженную на (-2), к третьей — первую, умноженную на (-3), к четвертой — первую, умноженную на (-1), получим

Разделим третью строку на 13 и поменяем местами вторую и третью строки:

Прибавим к третьей строке вторую, умноженную на (-9), к четвертой — вторую, умноженную на (-2):
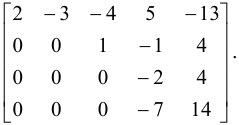
Разделив вторую строку на (-2), а третью на (-7), имеем:

Этой матрице соответствует система
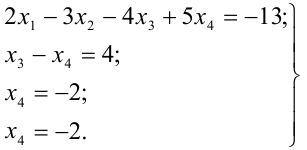
Осуществляя обратный ход, находим: 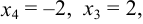
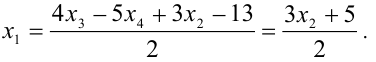
Таким образом, множеством решений будет
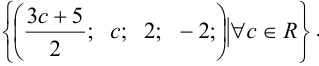
Задача №12.
Решить методом Гаусса систему уравнений
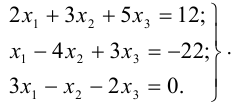
Решение:
Расширенная матрица системы имеет вид
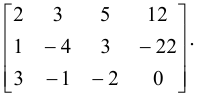
Поменяв местами первую и вторую строки, имеем
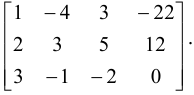
Прибавив ко второй строке первую, умноженную на (-2), а к третьей — первую, умноженную на (-3), получим
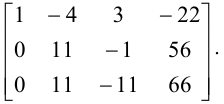
Прибавив к третьей строке вторую, умноженную на (-1), получим

Этой матрице соответствует система
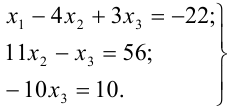
Осуществляя обратный ход, находим: 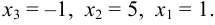
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

