Оглавление:
Решение произвольных систем
Базисными неизвестными совместной системы назовем те, коэффициенты при которых образуют базисный минор матрицы системы; остальные неизвестные назовем свободными.
Решение системы линейных уравнений производится следующим образом.
- Находим
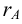 — ранг матрицы и
— ранг матрицы и 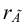 — ранг расширенной матрицы. Если
— ранг расширенной матрицы. Если 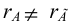 , то система несовместна.
, то система несовместна. - Если
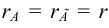 , то выделяем базисный минор и базисные неизвестные.
, то выделяем базисный минор и базисные неизвестные. - Данную систему заменяем равносильной, состоящей из тех
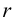 уравнений, в которые вошли элементы базисного минора.
уравнений, в которые вошли элементы базисного минора. - Если
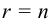 , т. е. число имеет единственное решение, которое можно найти по формулам Крамера.
, т. е. число имеет единственное решение, которое можно найти по формулам Крамера.
Если 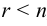 , т. е. число базисных неизвестных меньше числа неизвестных системы, то из системы, полученной в пункте 3, находим выражение базисных неизвестных через свободные, используя, например, формулы Крамера. Придавая свободным неизвестным произвольные значения, получим бесконечно много решений исходной системы.
, т. е. число базисных неизвестных меньше числа неизвестных системы, то из системы, полученной в пункте 3, находим выражение базисных неизвестных через свободные, используя, например, формулы Крамера. Придавая свободным неизвестным произвольные значения, получим бесконечно много решений исходной системы.
Задача №10.
Решить систему
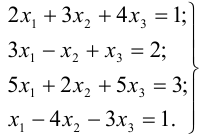
Решение:
1. Находим ранги матриц
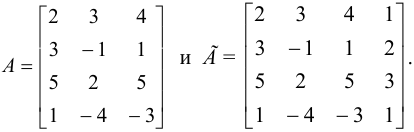
Получим 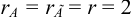 . Следовательно, система совместна.
. Следовательно, система совместна.
2. В качестве базисного минора можно взять, например, минор 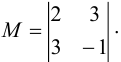
Тогда базисными неизвестными будут 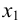 и
и 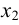 .
.
3. Данная система равносильна системе
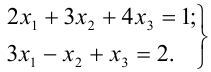
4. В данном случае  . Запишем последнюю систему в виде
. Запишем последнюю систему в виде
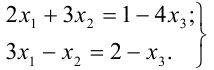
По формулам Крамера находим
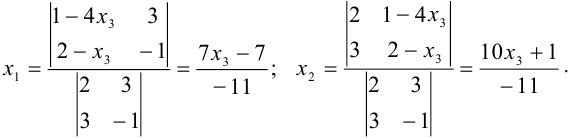
Следовательно, множество решений имеет вид
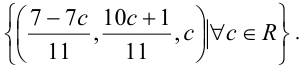
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

