Оглавление:
Вычисление определенных интегралов
Разложение функций в степенные ряды дает инструмент, позволяющий весьма эффективно вычислить приближенные значения определенных интегралов, в том числе и так называемых «неберущихся». При вычислении значения определенного интеграла от функции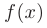 
, в случае, если 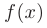разлагается в ряд Маклорена, ее разложение можно интегрировать почленно внутри интервала сходимости. С ростом числа членов, учитываемых в разложении функции 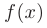, ошибка интегрирования снижается, а точность — возрастает.
Если 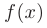в точке 
представляет собой знакочередующийся ряд, удовлетворяющий признаку Лейбница, то погрешность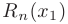 
приближенного значения 
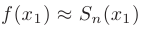не превышает по абсолютной величине модуля первого отброшенного члена:
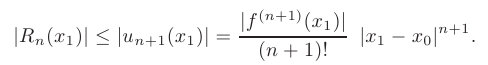
Пример:
Вычислить указанный определенный интеграл с точностью до 0,001 с помощью разложения подынтегральной функции в степенной ряд
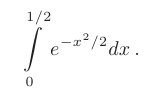
► Выполним разложение подынтегральной функции в ряд Маклорена с помощью замены переменной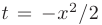 
в разложении табличной функции 
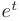(см. приложение В. 13):
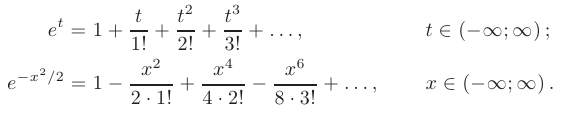
Интегрируя обе части полученного равенства на отрезке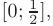 
лежащем внутри интервала сходимости 
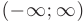, получим:
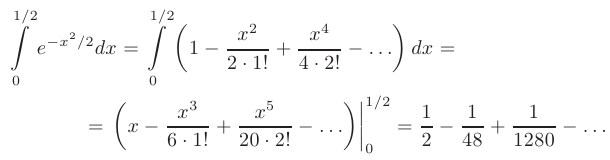
Получаем знакочередующийся числовой ряд, удовлетворяющий признаку Лейбница, а так как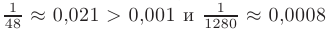 
< 0,001, то с точностью до 0,001 имеем:
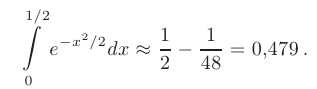
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Функциональные и степенные ряды в математике |
| Ряды Тейлора и Маклорена в математике |
| Решение дифференциальных уравнений при помощи степенных рядов |
| Матрица в математике |
