Оглавление:
Вычисление площади плоской фигуры
Пусть область 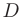 ограничена линиями:
ограничена линиями:
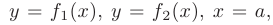
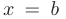
так, что
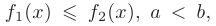
где
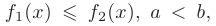
функции, непрерывные на отрезке 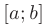 оси
оси 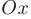 . В этом случае площадь области
. В этом случае площадь области 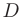 определяется формулой:
определяется формулой:
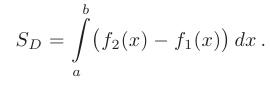
Это соотношение опирается на геометрический смысл определенного интеграла.
Аналогично, если область 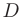 имеет границу, определяемую линиями:
имеет границу, определяемую линиями:
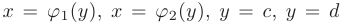
так, что
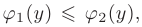
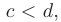
где 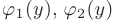 — функции, непрерывные на отрезке
— функции, непрерывные на отрезке 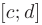 оси
оси 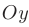 . В этом случае площадь области
. В этом случае площадь области 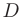 определяется формулой:
определяется формулой:
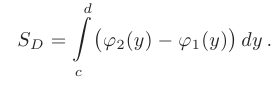
Пример:
Вычислить площадь замкнутой области, ограниченной линиями:
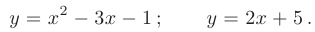
Указание. Все указанные линии и характерные точки построить в системе координат 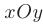 .
.
► Уточним расположение заданной области в системе координат 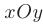 . Вначале найдем координаты точек пересечения графиков заданных функций:
. Вначале найдем координаты точек пересечения графиков заданных функций:
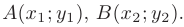
Для этого объединим уравнения в систему и решим ее:
Для построения заданной области в системе координат 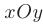 уточним координаты вершины параболы
уточним координаты вершины параболы
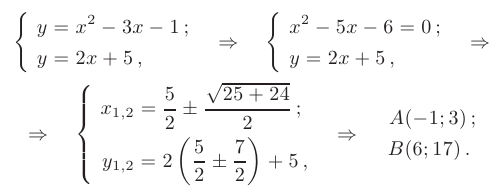
точки 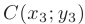 . Приведем уравнение параболы к каноническому виду:
. Приведем уравнение параболы к каноническому виду:
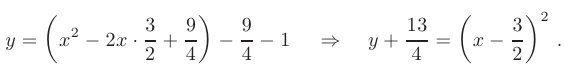
Слагаемые при переменных 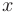 и
и 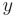 указывают на координаты вершины параболы:
указывают на координаты вершины параболы:
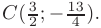
Искомая область в системе координат 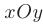 построена на рис. 6.3.
построена на рис. 6.3.
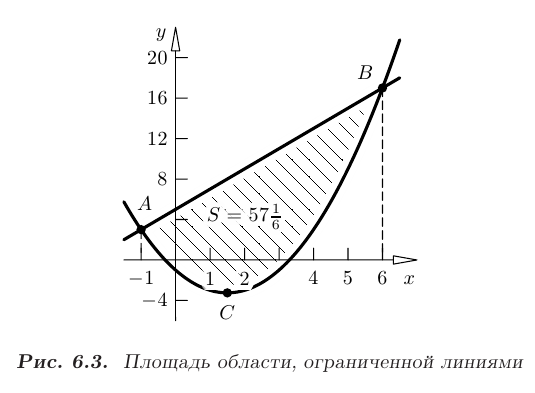
Площадь области, ограниченной сверху и снизу графиками функций
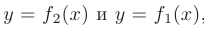
вычисляется по формуле
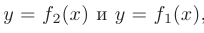
В нашем случае:
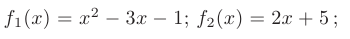
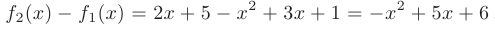
Тогда искомое значение площади замкнутой области:
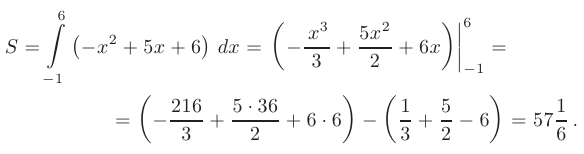
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:

