Обобщим понятие определенного интеграла на случай, когда либо один из концов (или оба) отрезка интегрирования бесконечно удален, либо функция не ограничена на отрезке интегрирования.
Несобственным интегралом 1-го рода называется интеграл по полубесконечному или бесконечному промежутку интегрирования, который определяется одним из следующих способов:
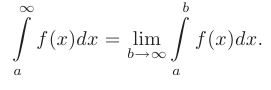
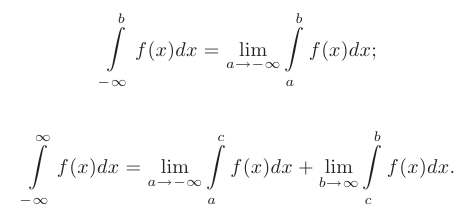
Если пределы, стоящие в правой части равенств существуют и конечны, то несобственные интегралы называют сходящимися, в противном случае — расходящимися.
Несобственным интегралом 2-го рода называется интеграл от функции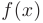 
, непрерывной на полуинтервалах 
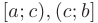и имеющей разрыв 2-го рода при 
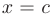, который определяется формулой
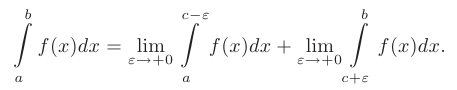
Так же, как и выше, несобственный интеграл называется сходящимся, если оба предела существуют и конечны. В противном случае несобственный интеграл называется расходящимся.
Если же точка разрыва с находится на конце промежутка, то:
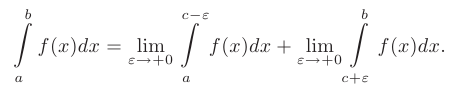
Пример:
Вычислить несобственные интегралы или установить их расходимость:
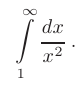
Данный интеграл является несобственным интегралом I-го рода
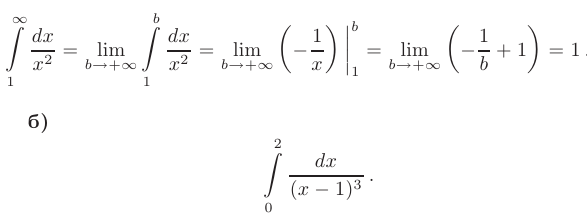
► Так как подынтегральная функция имеет разрыв 2-го рода в точке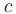 
= 1, лежащей внутри промежутка интегрирования [0;2], то данный интеграл является несобственным интегралом II-го рода:
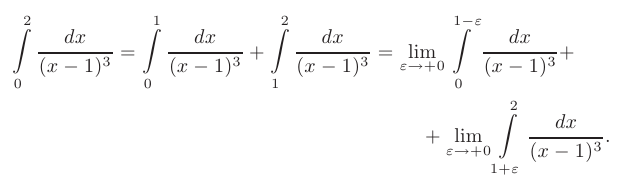
Вычислим каждый предел отдельно:
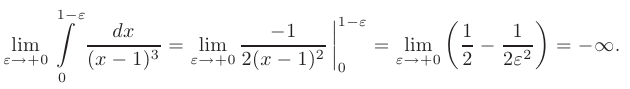
Следовательно, на отрезке [0,1] интеграл расходится.
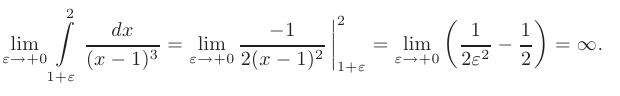
На отрезке [1; 2] интеграл также расходится. Таким образом, данный интеграл расходится на всем отрезке [0;2].
Заметим, что если вычислить данный интеграл, не обращая внимания на разрыв подынтегральной функции в точке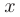 
= 1, то получили бы неверный результат. Действительно,
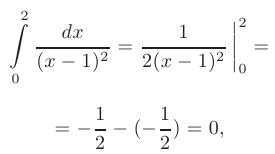
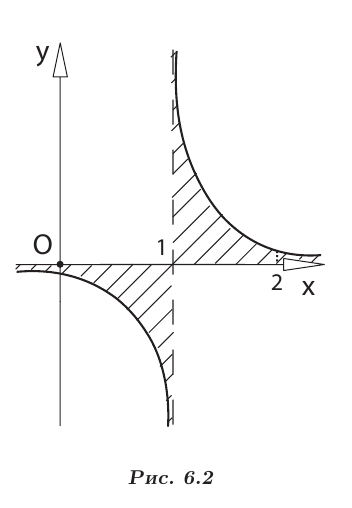
что невозможно, потому что площадь фигуры, ограниченной кривой
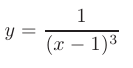
и отрезком [0; 2] оси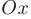 
неограничена (см. рис. 6.2).
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Интегрирование иррациональных функций в математике |
| Понятие определенного интеграла в математике |
| Вычисление площади плоской фигуры в математике |
| Обыкновенные дифференциальные уравнения в математике |
