Оглавление:
Понятие о функции многих переменных
Переменные 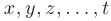 называются независимыми между собой, если каждая из них может принимать любые значения в своей области изменения, независимо от того, какие значения принимают при этом остальные переменные.
называются независимыми между собой, если каждая из них может принимать любые значения в своей области изменения, независимо от того, какие значения принимают при этом остальные переменные.
Переменная величина и называется функцией независимых переменных 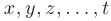 , если каждой совокупности значений этих переменных из области их изменения соответствует единственное определенное значение
, если каждой совокупности значений этих переменных из области их изменения соответствует единственное определенное значение 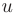 :
:
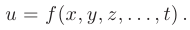
Областью определения функции 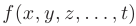 называется совокупность значений независимых переменных
называется совокупность значений независимых переменных 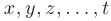 , при которых функция определена, т.е. принимает действительные значения.
, при которых функция определена, т.е. принимает действительные значения.
Пример:
Найти область определения функции:
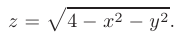
► Область определения данной функции задается неравенством 4 —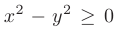 или
или 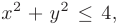 т.е. представляет собой круг радиуса
т.е. представляет собой круг радиуса 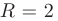 с центром в начале координат.
с центром в начале координат.
В экономической теории одним из базовых понятий является функция полезности 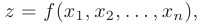 , выражающая полезность от
, выражающая полезность от 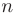 приобретенных товаров. Наиболее часто используются степенная и логарифмическая функции:
приобретенных товаров. Наиболее часто используются степенная и логарифмическая функции:
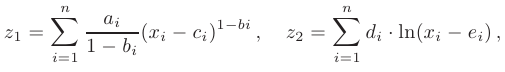
где
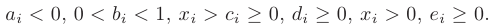
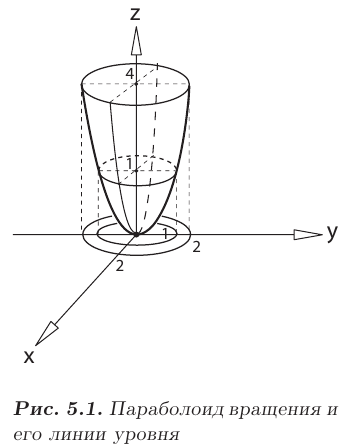
В дальнейшем для упрощения записей все определения и формулы приводятся только для функции двух независимых переменных.
Геометрическим изображением (графиком) функции двух переменных 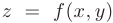 является поверхность в пространстве
является поверхность в пространстве 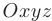 .
.
Линией уровня функции 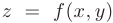 называется меожество всех точек плоскости
называется меожество всех точек плоскости 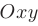 , для которых функция имеет одно и то же значение. Линии уровня задаются уравнением:
, для которых функция имеет одно и то же значение. Линии уровня задаются уравнением:
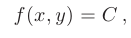
где 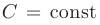 — некоторая постоянная.
— некоторая постоянная.
Примерами линий уровня являются параллели и меридианы на глобусе — это линии уровня функции широты и долготы. Изотермы — линии уровня функции температуры, изобары — линии уровня функции атмосферного давления. Другими примерами линий уровня являются контуры местности на топографических картах, которые образуются из точек с одинаковой высотой местности над уровнем моря. Для функции 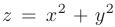 семейство линий уровня будет задаваться уравнением
семейство линий уровня будет задаваться уравнением 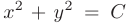 , где константа
, где константа 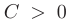 . Полученному уравнению соответствует семейство концентрических окружностей с центром в начале координат и радиусом
. Полученному уравнению соответствует семейство концентрических окружностей с центром в начале координат и радиусом 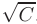 . Построив эти линии, легко увидеть, что функция
. Построив эти линии, легко увидеть, что функция 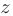 растет в радиальном направлении. Поэтому, геометрическим образом данной функции в пространстве будет «яма» с вогнутыми, быстро растущими краями. Точное название этой поверхности — параболоид вращения.
растет в радиальном направлении. Поэтому, геометрическим образом данной функции в пространстве будет «яма» с вогнутыми, быстро растущими краями. Точное название этой поверхности — параболоид вращения.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:

