Оглавление:
Максимум и минимум функции
Наличие у одной и той же функции интервалов возрастания и убывания порождает особые точки, отделяющие эти интервалы друг от друга и называемые точками экстремума.
Точка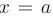 
называется точкой максимума (или точкой минимума) функции 
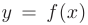, если существует такая 
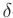-окрестность этой точки, что для всех 
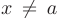из этой окрестности выполняется неравенство 
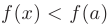(или 
).
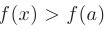Заметим, что понятие экстремума всегда связано с двусторонней окрестностью точки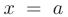 
из области определения функции 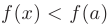. Поэтому функция 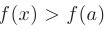может иметь экстремум лишь во внутренних точках области определения. Более того, непрерывная функция может иметь экстремум лишь в критических точках первого рода, в которых ее производная равна нулю или не существует.
Необходимое условие экстремума
Если дифференцируемая функция 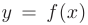имеет экстремум в точке 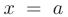, то ее производная в этой точке будет равна нулю:
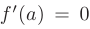. Геометрически это означает, что в точках экстремума касательная к графику функции 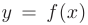параллельна оси 
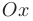(см. точки 
и 
на рис. 4.3 а)).
Первое достаточное условие экстремума
Если непрерывная функция 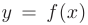дифференцируема в достаточно малой окрестности критической точки 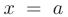и при переходе через нее производная меняет знак с минуса на плюс (или с плюса на минус), то точка 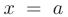является точкой минимума (или максимума) функции .
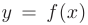Второе достаточное условие экстремума
Если в точке 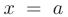первая производная функции 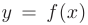равна нулю 
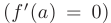, а вторая производная в этой точке существует и отлична от нуля 
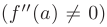, то при 
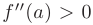(или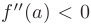 
) точка 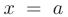является точкой минимума (или максимума) функции .
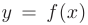Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Правило Лопиталя в математике |
| Возрастание и убывание функции в математике |
| Наибольшее и наименьшее значение функции на отрезке в математике |
| Выпуклость графика функции. Точки перегиба в математике |
