Линейная зависимость и координаты векторов
Линейной комбинацией векторов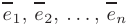 
называют сумму их произведений на произвольные действительные числа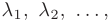 
:
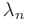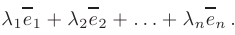
Векторы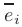 
называются линейно зависимыми, если существуют такие действительные числа 
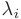, не равные одновременно нулю, при которых линейная комбинация указанных векторов обращается в нуль:
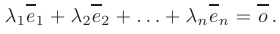
Если линейная комбинация векторов обращается в нуль лишь при
то векторы 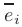называются линейно независимыми.
Заметим, что если хотя бы один из векторов 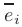, равен нулевому вектору 
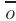, то система векторов будет линейно зависимой.
Можно доказать, что каждый вектор на некоторой прямой можно представить единственным способом в виде
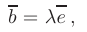
где вектор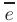 
называется базисом данной прямой, а число 
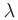— координатой вектора
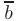в базисе .
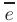Аналогично предыдущему можно доказать, что каждый вектор на некоторой плоскости можно представить единственным способом в виде
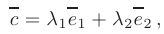
где упорядоченная пара неколлинеарных (т.е. линейно независимых) векторов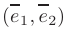 
называется базисом данной плоскости, а числа 
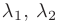— координатами вектора 
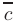в базисе .
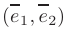Тогда каждый вектор трехмерного пространства можно представить единственным способом в виде
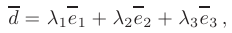
где упорядоченная тройка некомпланарных (т.е. линейно независимых) векторов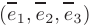 
называется базисом данного пространства, а числа 
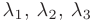— координатами вектора 
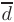в базисе .
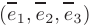Заметим, что запись произвольного вектора 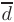в виде линейной комбинации векторов базиса 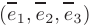называется разложением вектора по базису.
Часто используют стандартный базис из взаимно перпендикулярных единичных векторов, обозначаемый как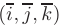 
(см. рис. 2.3). В декартовой прямоугольной системе координат векторы 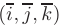со-направлены с соответствующими осями координат 
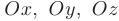и называются ортами. Тогда любой вектор 
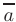единственным образом можно представить в виде их линейной комбинации с коэффициентами 
:
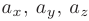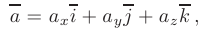
где числа 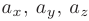— координаты вектора 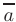в базисе 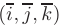. С другой стороны, координаты 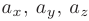вектора 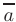— это его проекции на соответствующие координатные оси. Вектор 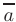с координатами 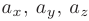записывают в виде 
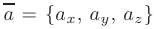. Длина вектора а определяется по формуле
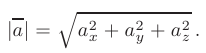
При известных координатах точек
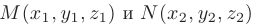
координаты вектора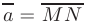 
вычисляются по формуле
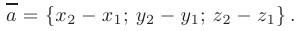
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Декартовы координаты в математике |
| Векторы и операции над ними в математике |
| Линейные операции над векторами в координатной форме в математике |
| Уравнение прямой на плоскости в математике |
