Оглавление:
Собственные значения и собственные векторы матрицы
Число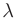 
называется собственным значением квадратной матрицы 
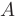порядка 
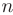, если существует такой ненулевой 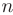-мерный вектор 
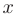, что выполняется равенство 
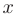. При этом вектор называется собственным вектором матрицы 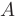, принадлежащим ее собственному значению .
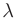Множество всех собственных значений матрицы 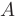совпадает с множеством всех решений уравнения 
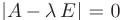, которое называется характеристическим уравнением матрицы 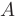. Множество всех собственных векторов матрицы 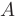, принадлежащих ее собственному значению 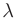, совпадает с множеством всех ненулевых решений системы однородных уравнений 
.
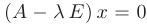Можно доказать, что если квадратная матрица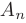 
имеет 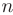различных собственных значений, то отвечающие им собственные
векторы линейно независимы, а матрица 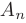в базисе её собственных векторов является диагональной:
Пример:
Найти собственные значения и собственные векторы матрицы
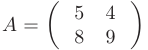
и привести ее к диагональному виду. ► Составим характеристическое уравнение матрицы :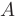
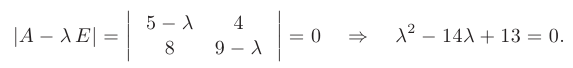
Следовательно, матрица 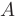имеет два собственных значения 
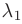= 1, 
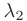= 13.
Для определения координат собственных векторов получим две системы линейных уравнений. Решая их, определим множество допустимых решений.
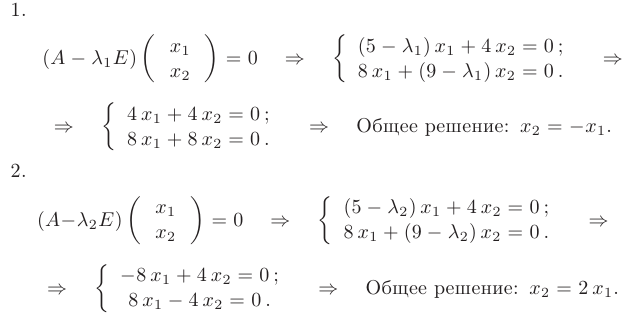
Полагая в общем решении системы 1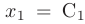 
, получим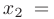 
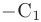где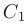 
— произвольная постоянная. Следовательно, собственному значению 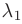= 1 соответствует семейство собственных векторов 
.
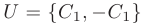Полагая в общем решении системы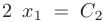 
, получим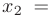 
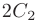. Следовательно, собственному значению 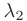= 13 соответствует семейство собственных векторов 
.
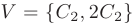В базисе из любых пар собственных векторов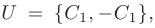 
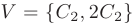(т. е. при любых 
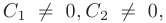например, при 
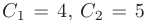из векторов 
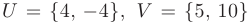) матрица 
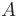будет иметь вид
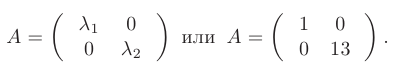
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Ранг матрицы в математике |
| Системы линейных уравнений m*n в математике |
| Квадратичные формы в матричной записи в математике |
| Декартовы координаты в математике |
