Оглавление:
Формулы приведения
Наиболее употребительными являются следующие формулы:
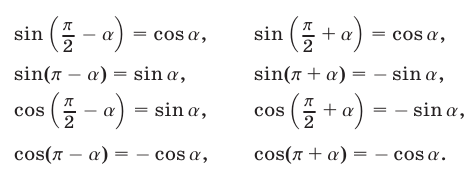
Любую из формул приведения можно получить, пользуясь следующими правилами:
а) если аргумент приводимой функции равен 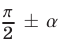 или
или 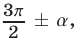 то синус заменяется на косинус, а косинус — на синус; если же аргумент приводимой функции равен
то синус заменяется на косинус, а косинус — на синус; если же аргумент приводимой функции равен 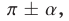 то функция не меняет своего названия;
то функция не меняет своего названия;
б) перед приведенной функцией ставится такой же знак, какой имеет приводимая функция, если считать, что 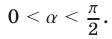
Формулы суммы и разности синусов:
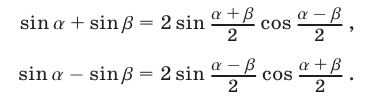
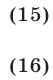
Формулы суммы и разности косинусов:
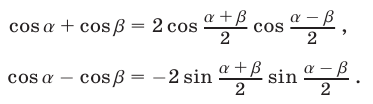
Формулы суммы и разности тангенсов:
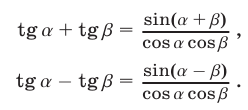
Пример №39.
Преобразовать в произведение тригонометрических функций сумму:
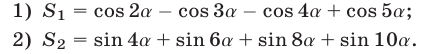
Решение:
Воспользуемся формулами (15)-(18).
1) Так как
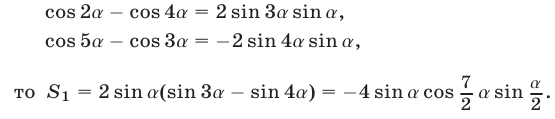
2) Так как
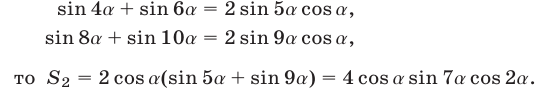
Пример №41.
Доказать тождество
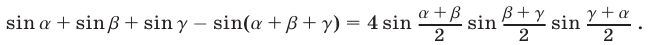
Доказательство. Пусть S — левая часть тождества. Преобразуем S, пользуясь формулами (15)-(18). Имеем
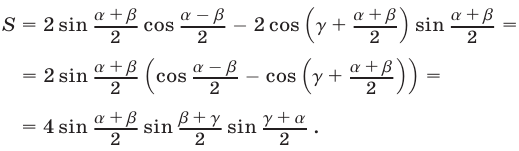
Пример №46.
Доказать, что если 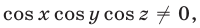 то справедливо равенство
то справедливо равенство
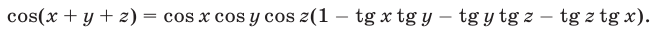
Доказательство. Применяя формулы косинуса и синуса суммы (формулы сложения), получаем равенство
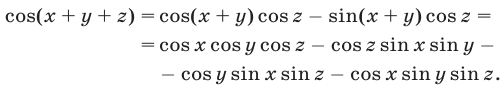
Для завершения доказательства следует правую часть этого равенства умножить и разделить на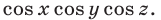
Пример №48.
Вычислить без таблиц суммы: 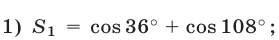
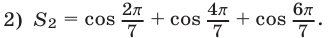
Решение:
1) Применяя формулу суммы косинусов, получаем

Следовательно, 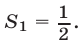
2) Нетрудно убедиться в том, что применение формулы суммы косинусов не позволяет вычислить 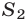 . Преобразуем сумму
. Преобразуем сумму 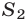 в произведение. Рассмотрим равенство
в произведение. Рассмотрим равенство
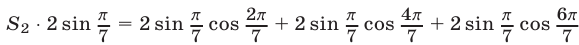
и преобразуем правую часть этого равенства. Получим
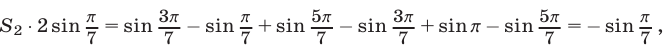
откуда
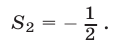
Пример №50.
Доказать тождество
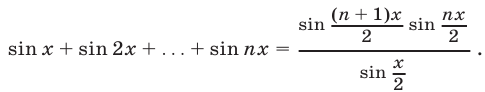
Доказательство. Пусть 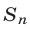 — левая часть равенства. Умножим
— левая часть равенства. Умножим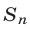 на
на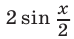 и воспользуемся формулой
и воспользуемся формулой 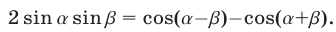 Получим
Получим
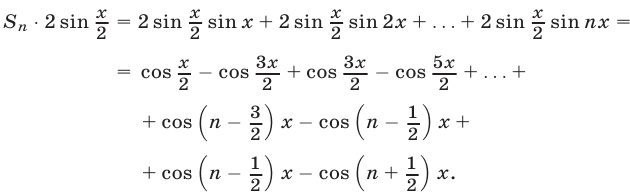
В этой сумме взаимно уничтожаются все слагаемые, кроме первого и последнего. Поэтому
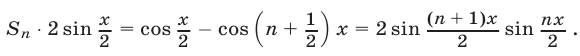
Если 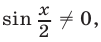 то из последнего равенства находим
то из последнего равенства находим
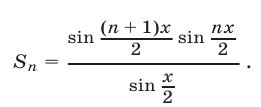
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

