Оглавление:
Примеры с решениями
Пример №323.
Изобразить на координатной плоскости 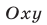 фигуру
фигуру 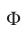 , заданную системой неравенств, и найти площадь
, заданную системой неравенств, и найти площадь 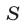 этой фигуры.
этой фигуры.
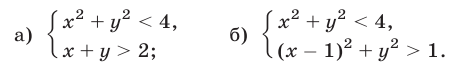
Решение:
а) Неравенство 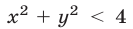 задает множество точек, лежащих внутри окружности с центром в начале координат и радиусом 2 (рис. 27.1), а неравенство
задает множество точек, лежащих внутри окружности с центром в начале координат и радиусом 2 (рис. 27.1), а неравенство 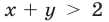 — множество точек, расположенных выше прямой
— множество точек, расположенных выше прямой 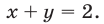
Эта прямая пересекает окружность в точках 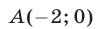 и
и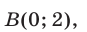 а фигура
а фигура 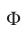 представляет собой сегмент (рис. 27.1). Искомая площадь
представляет собой сегмент (рис. 27.1). Искомая площадь 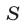 равна разности между площадью
равна разности между площадью 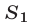 четверти круга и площадью
четверти круга и площадью 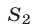 треугольника
треугольника 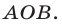
Так как 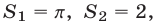 то
то 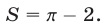
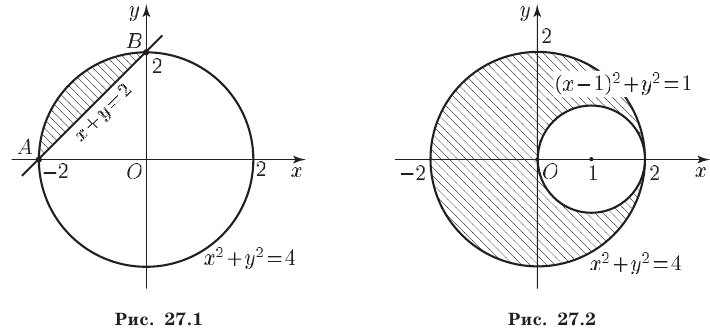
б) Фигура 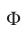 — это множество точек, лежащих внутри окружности с центром в точке
— это множество точек, лежащих внутри окружности с центром в точке 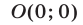 и радиусом 2, но вне окружности с центром в точке
и радиусом 2, но вне окружности с центром в точке 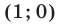 и радиусом 1 (рис. 27.2). Значит, площадь фигуры
и радиусом 1 (рис. 27.2). Значит, площадь фигуры 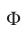 равна
равна 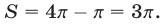
Пример №324.
Найти площадь фигуры 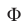 , которая задается на координатной плоскости системой неравенств
, которая задается на координатной плоскости системой неравенств
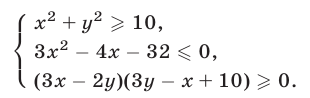
Решение:
Неравенство (1) определяет множество точек, лежащих вне и на границе круга с центром в точке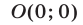 и радиусом
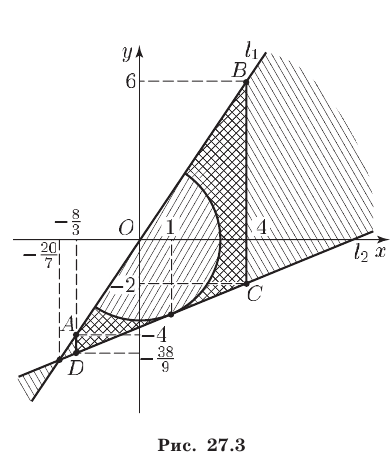
и радиусом 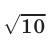 (рис. 27.3).
(рис. 27.3).
Решив неравенство (2), получим 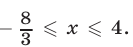 Поэтому неравенство (2) задает вертикальную полосу, лежащую между прямыми
Поэтому неравенство (2) задает вертикальную полосу, лежащую между прямыми  и
и 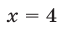 (включая и точки этих прямых).
(включая и точки этих прямых).
Наконец, неравенству (3) удовлетворяют точки множества 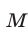 , которое состоит из двух острых вертикальных углов, образованных прямыми
, которое состоит из двух острых вертикальных углов, образованных прямыми 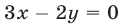 и
и 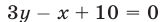 (включая и точки этих прямых), так как в точке
(включая и точки этих прямых), так как в точке 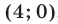 принадлежащей множеству
принадлежащей множеству 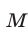 , левая часть неравенства (3) положительна. Множество
, левая часть неравенства (3) положительна. Множество 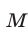 заштриховано на рис. 27.3, а указанные прямые обозначены
заштриховано на рис. 27.3, а указанные прямые обозначены 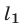 и
и 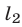 .
.
Прямая 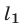 пересекается с прямыми
пересекается с прямыми 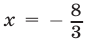 и
и 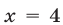 в точках
в точках 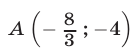 и
и 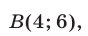 , а прямая
, а прямая 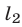 пересекается с теми же прямыми в точках
пересекается с теми же прямыми в точках 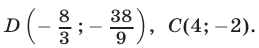 Далее, прямая
Далее, прямая 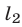 касается окружности
касается окружности 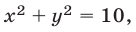 так как система уравнений
так как система уравнений
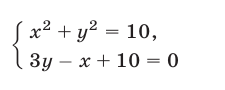
имеет единственное решение 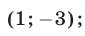 наконец, прямая
наконец, прямая 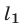 проходит через центр этой окружности.
проходит через центр этой окружности.
Итак, фигура 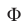 — это трапеция
— это трапеция 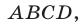 из которой удален полукруг радиуса
из которой удален полукруг радиуса 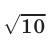 с центром в точке
с центром в точке 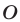 . Искомая площадь
. Искомая площадь
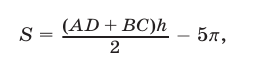
где 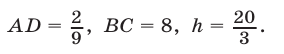
Ответ.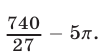
Пример №325.
На координатной плоскости рассматривается фигура 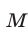 , состоящая из всех точек, координаты которых удовлетворяют системе неравенств
, состоящая из всех точек, координаты которых удовлетворяют системе неравенств
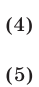
Изобразить фигуру 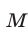 и найти ее площадь.
и найти ее площадь.
Решение:
Неравенство (5), равносильное неравенству
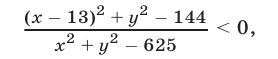
является верным в тех и только в тех точках плоскости 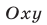 , которые лежат вне круга радиуса 12 с центром
, которые лежат вне круга радиуса 12 с центром 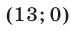 и внутри круга радиуса 25 с центром в точке
и внутри круга радиуса 25 с центром в точке 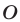 (рис. 27.4). Неравенство (4) имеет смысл, если
(рис. 27.4). Неравенство (4) имеет смысл, если
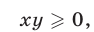
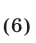
т. е. для точек I и III квадрантов. Считая условие (6) выполненным, рассмотрим два возможных случая: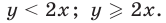
1) Если
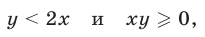
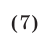
то неравенство (4) является верным. Система неравенств (7) задает множество точек I и III квадрантов, лежащих ниже прямой 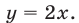
2) Если
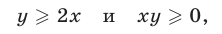
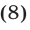
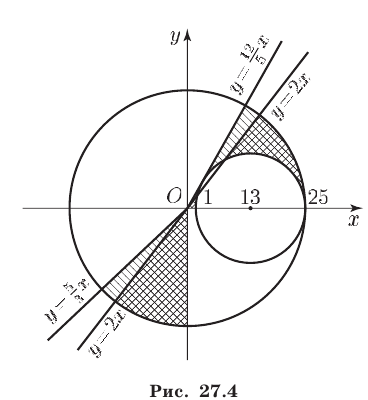
то неравенство (4) равносильно каждому из неравенств
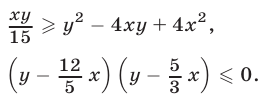
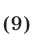
Условиями (8), (9) определяется множество тех точек I квадранта, которые заключены между прямыми 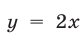 и
и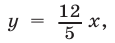 и точек III квадранта, которые заключены между прямыми
и точек III квадранта, которые заключены между прямыми 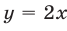 и
и 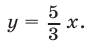
Заметим, что прямая 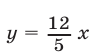 имеет единственную общую точку с окружностью
имеет единственную общую точку с окружностью 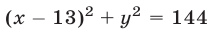 и, следовательно, касается этой окружности. Площадь
и, следовательно, касается этой окружности. Площадь 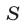 фигуры
фигуры 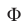 равна
равна 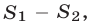 где
где 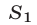 —сумма площадей двух секторов (им соответствуют центральные углы
—сумма площадей двух секторов (им соответствуют центральные углы 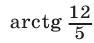 и
и 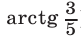 ), a
), a 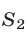 — площадь полукруга радиуса 12.
— площадь полукруга радиуса 12.
Ответ.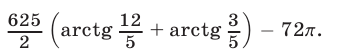
Пример №326.
Найти площадь фигуры 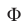 , которая задается на координатной плоскости системой неравенств
, которая задается на координатной плоскости системой неравенств
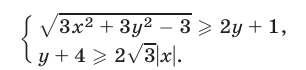
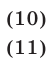
Решение:
Область определения неравенства (10), а значит, и системы (10), (11) задается условием 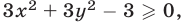 т. е.
т. е.
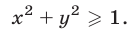
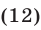
Неравенство (12) определяет область, внешнюю по отношению к кругу с центром в начале координат и радиусом 1 (включая границу круга, рис. 27.5).
Возможны два случая: 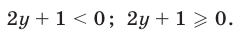
1) Если 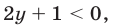 т. е.
т. е.

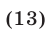
то неравенство (10) является верным на множестве 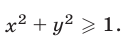
2) Если 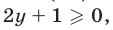 т. е.
т. е.
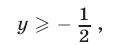
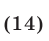
то неравенство (10) равносильно каждому из неравенств
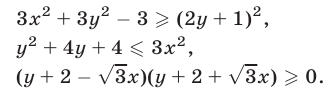
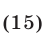
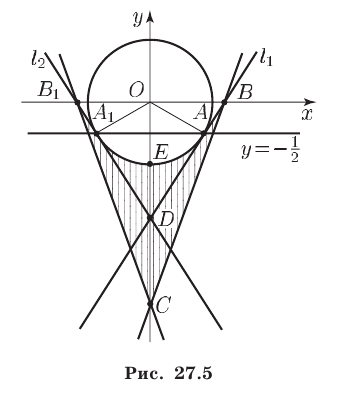
Прямые 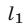 и
и 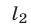 заданные соответственно уравнениями
заданные соответственно уравнениями

проходят через точку 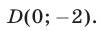 Прямая
Прямая 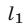 касается окружности
касается окружности 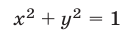 в точке
в точке 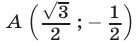 так как система уравнений
так как система уравнений
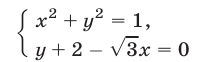
имеет единственное решение 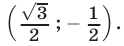 Прямая I2, симметричная прямой относительно оси
Прямая I2, симметричная прямой относительно оси 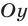 , касается этой же окружности в точке
, касается этой же окружности в точке 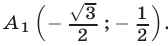
В точке 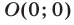 левая часть неравенства (15) положительна и поэтому указанное неравенство справедливо в двух вертикальных углах с вершиной в точке
левая часть неравенства (15) положительна и поэтому указанное неравенство справедливо в двух вертикальных углах с вершиной в точке 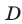 , содержащих ось
, содержащих ось 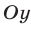 .
.
Рассмотрим неравенство (11). Уравнение
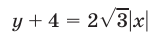
задает два луча, выходящие из точки 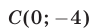 и пересекающиеся прямые
и пересекающиеся прямые 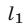 и
и 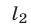 в точках
в точках 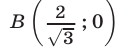 и
и 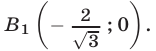 Неравенству (11) удовлетворяют точки, находящиеся внутри и на границе угла
Неравенству (11) удовлетворяют точки, находящиеся внутри и на границе угла 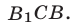
Итак, множеством точек, удовлетворяющих системе неравенств (10), (11) является фигура 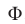 , выделенная штриховкой на рис. 27.5. Ее граница состоит из отрезков
, выделенная штриховкой на рис. 27.5. Ее граница состоит из отрезков 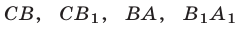 и дуги
и дуги 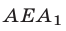 окружности
окружности 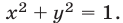
Площадь фигуры 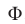 равна
равна
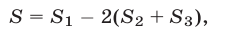
где 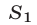 —площадь треугольника
—площадь треугольника 
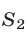 — площадь треугольника
— площадь треугольника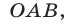
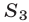 — площадь сектора
— площадь сектора 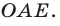 Здесь
Здесь
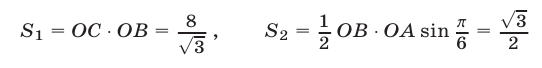
(так как 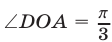 ),
),
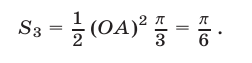
Ответ. 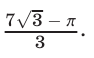
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

