Оглавление:
Уравнения, неравенства и системы неравенств с двумя переменными, содержащие знак модуля
Примеры с решениями
Пример №319.
Найти множество точек координатной плоскости 
, координаты 
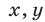которых удовлетворяют уравнению:
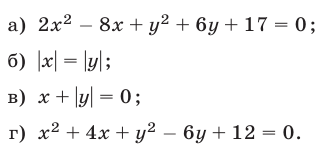
Решение:
а) Запишем уравнение в виде
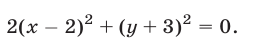
Это уравнение имеет единственное решение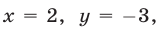 
т. е. данному уравнению удовлетворяют координаты только одной точки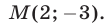
б) Уравнение равносильно совокупности уравнени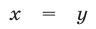й 
и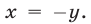 
Искомое множество состоит из всех точек, принадлежащих биссектрисам I и III, а также II и IV координатных углов (рис. 26.11).
в) Уравнение равносильно совокупности двух систем:
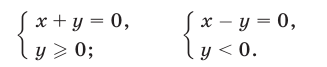
Первой из них удовлетворяют точки, принадлежащие биссектрисе II координатного угла, второй системе — точки, принадлежащие биссектрисе III координатного угла (рис. 26.12).
г) Запишем уравнение в виде
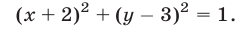
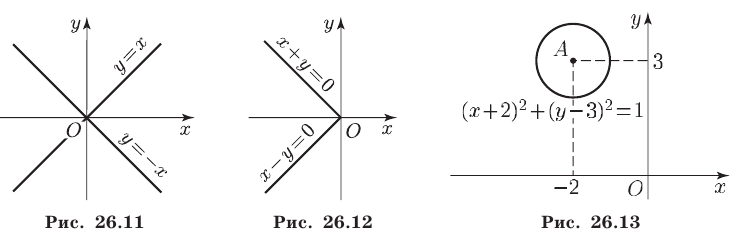
Это уравнение окружности с центром в точке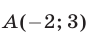 
и радиусом 1 (рис. 26.13).
Пример №320.
Изобразить на координатной плоскости 
фигуру 
, координаты точек которой удовлетворяют системе неравенств
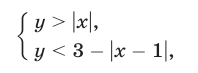
и найти площадь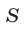 
этой фигуры.
Решение:
Построим графики функци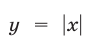й 
и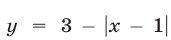 
(рис. 26.14).
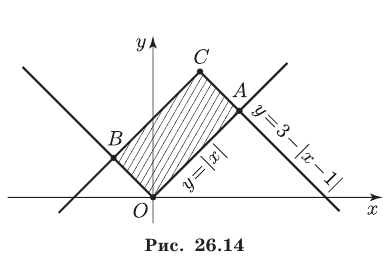
Решив систему уравнений
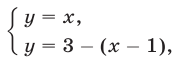
находим общую точку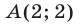 
этих графиков, лежащую в I квадранте (рис. 26.14). Аналогично, решив систему уравнений
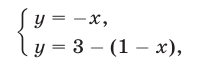
находим общую точку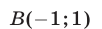 
графиков функци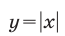й 
и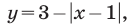 
лежащую во II квадранте.
Неравенству (1) удовлетворяют все точки координатной плоскости, расположенные выше графика функции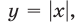 
а неравенству (2) — все точки координатной плоскости, лежащие ниже графика функции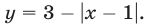 
Следовательно, системе (1), (2) удовлетворяют все точки, лежащие внутри прямоугольника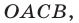 
полученного при пересечении графиков функци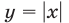й 
и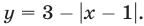 
Так как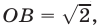 
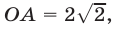то
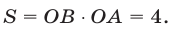
Пример №321.
Найти все такие пары целых чисел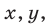 
которые удовлетворяют системе неравенств
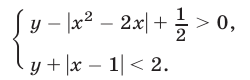
Решение:
Запишем данную систему в следующем виде:
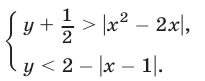
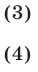
Так как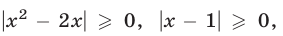 
то из неравенств (3) и (4) следует, что
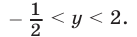
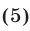
Целыми числами, удовлетворяющими неравенству (5), являются лишь 0 и 1, поэтому система (3), (4) может иметь целые решения только пр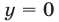и 
и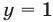 
.
1) Если 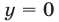, то система (3), (4) примет вид
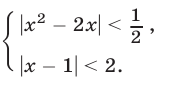
Второму из этих неравенств удовлетворяют целые числа 0, 1 и 2. Проверка показывает, что первому неравенству удовлетворяют
лишь 0 и 2. Следовательно, пары чисел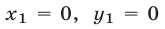 
и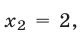 
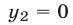образуют решения исходной системы неравенств.
2) Если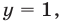 
то система (3), (4) приводится к виду
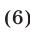
Второму неравенству системы (6) удовлетворяет единственное целое число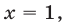 
которое является также и решением первого неравенства.
Ответ.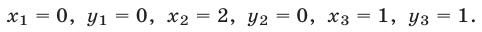 
Пример №322.
Изобразить на координатной плоскости фигуру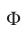 
, координаты 
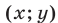точек которой определяются неравенством
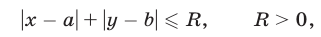
и найти площадь 
фигуры .
Решение:
1) Рассмотрим сначала случай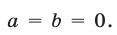 
Тогда неравенство (7) примет вид
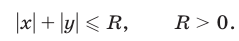
Если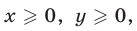 
то неравенство (8) можно записать так:
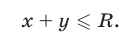
Множество точек, удовлетворяющих условиям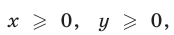 
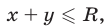— это треугольник 
образованный прямой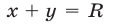 
(рис. 26.15) и координатными полуосями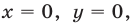 
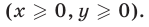
Если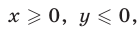 
то неравенство (8) примет вид
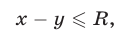
а множество точек таких, что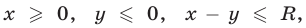 
— это треугольник 
симметричный треугольнику 
относительно оси 
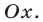
Аналогично рассматриваются случа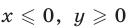и 
и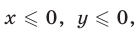 
которым соответствуют треугольники 
и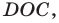 
симметричные соответственно треугольникам 
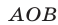и 
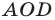относительно оси 
.
Таким образом, фигура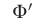
, определяемая неравенством (8), представляет собой квадрат с центром в точке 
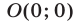и вершинами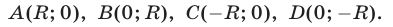 
Заметим, что симметрия фигуры 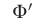относительно координатных осей следует из того, что наряду с точкой 
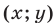этой фигуре принадлежат точки 
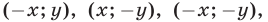так как 
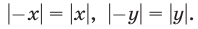Площадь этой фигуры равна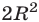 
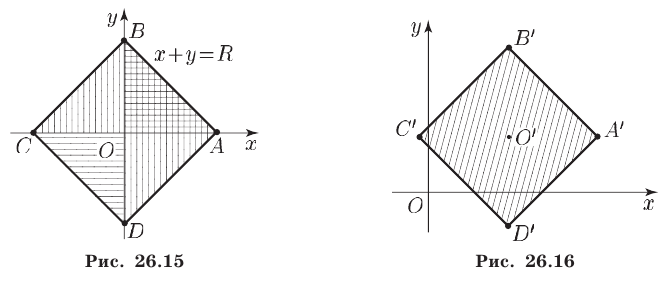
2) Рассмотрим теперь неравенство (7). Так как фигуру 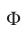, определяемую неравенством (7), можно получить из фигуры 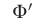, заданной неравенством (8), с помощью параллельного переноса (сдвига на вектор 
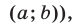то 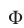— квадрат (рис. 26.16) с центром в точке 
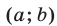и вершинами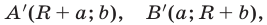 
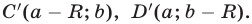
Площадь фигуры , как и фигуры 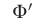, равна .
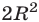Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
