Оглавление:
Тригонометрические неравенства
Рассмотрим примеры тригонометрических неравенств. При решении таких неравенств используются свойства тригонометрических функций и их графики.
Примеры с решениями
Пример №303.
Решить неравенство
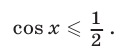
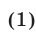
Решение:
Первый способ. Построим график функции 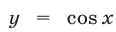 и проведем прямую
и проведем прямую 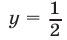 (рис. 25.1).
(рис. 25.1).
Решить неравенство (1) — значит найти все значения 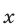 , при которых соответствующие точки графика функции
, при которых соответствующие точки графика функции 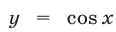 лежат ниже прямой
лежат ниже прямой 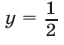 и на этой прямой.
и на этой прямой.
Так как функция 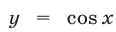 является периодической с периодом
является периодической с периодом 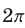 , то достаточно найти решения неравенства (1) на отрезке длиной
, то достаточно найти решения неравенства (1) на отрезке длиной 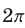 . В качестве такого отрезка возьмем отрезок
. В качестве такого отрезка возьмем отрезок 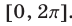
Прямая 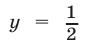 при
при 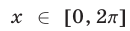 пересекает график функции
пересекает график функции 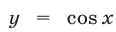 в точках
в точках 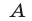 и
и 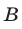 (рис. 25.1), абсциссы которых служат
(рис. 25.1), абсциссы которых служат
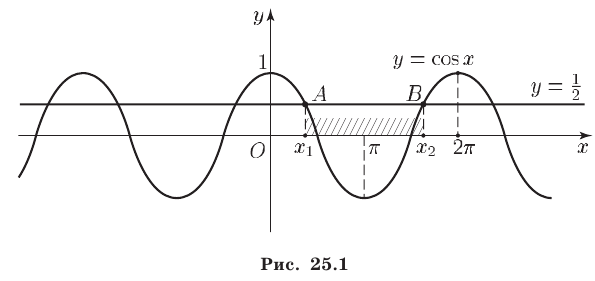
корнями уравнения  на отрезке
на отрезке 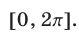 Одним из корней этого уравнения является
Одним из корней этого уравнения является 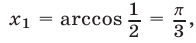 другим — значение
другим — значение 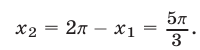
Следовательно, значения 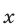 из отрезка
из отрезка 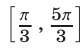 и значения, являются решениями неравенства (1) на отрезке
и значения, являются решениями неравенства (1) на отрезке 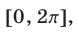 а множество всех решений неравенства (1) — это объединение всех отрезков каждый из которых получается из отрезка
а множество всех решений неравенства (1) — это объединение всех отрезков каждый из которых получается из отрезка  сдвигом по оси
сдвигом по оси 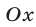 на
на 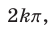 где
где 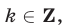 т. е. совокупность отрезков вида
т. е. совокупность отрезков вида
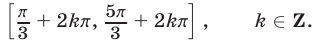
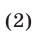
Ответ. 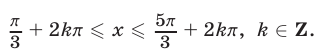
Второй способ. Решим неравенство (1) с помощью единичной окружности. Построим угол, косинус которого равен 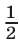 . Для этого отметим на оси
. Для этого отметим на оси 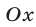 точку с абсциссой, равной
точку с абсциссой, равной 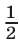 , и проведем через эту точку прямую
, и проведем через эту точку прямую 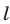 , параллельную оси
, параллельную оси 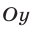 (рис. 25.2).
(рис. 25.2).
Прямая 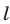 пересекает единичную окружность в точках
пересекает единичную окружность в точках 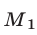 и
и 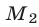 .
.
Точке 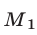 соответствует угол в
соответствует угол в 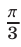 радиан, а точке
радиан, а точке 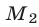 — угол в
— угол в 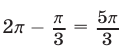 радиан.
радиан.
Из рис. 25.2 видно, что абсциссу, меньшую или равную 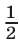 , имеют все точки единичной окружности, расположенные слева от прямой
, имеют все точки единичной окружности, расположенные слева от прямой 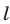 и на самой прямой. Итак, множество всех решений неравенства (1) представляет собой совокупность отрезков вида (2).
и на самой прямой. Итак, множество всех решений неравенства (1) представляет собой совокупность отрезков вида (2).
Пример №304.
Решить неравенство
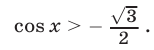
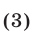
Решение:
Построим график функции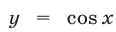 на отрезке
на отрезке 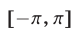 и проведем прямую
и проведем прямую 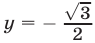 рис. 25.3).
рис. 25.3).
Эта прямая пересекает график функции 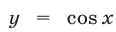 ,
, 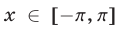 в точках
в точках 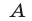 и
и 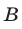 , абсциссы
, абсциссы 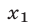 и
и 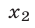 которых равны
которых равны 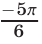 и
и 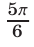 соответственно. Из рис. 25.3 видно, что решения неравенства (3) на отрезке
соответственно. Из рис. 25.3 видно, что решения неравенства (3) на отрезке 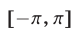 образуют интервал
образуют интервал 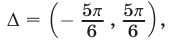 а множество всех решений неравенства (3) — это совокупность интервалов, каждый
а множество всех решений неравенства (3) — это совокупность интервалов, каждый
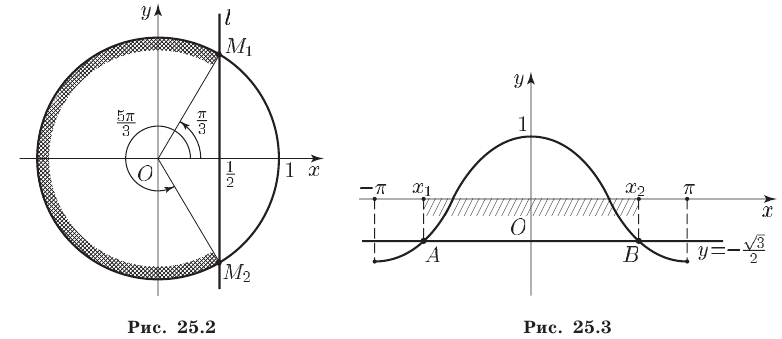
из которых можно получить сдвигом интервала  по оси
по оси 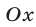 на
на 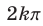 , где
, где 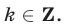
Ответ. 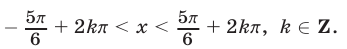
Пример №305.
Решить неравенство
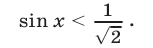
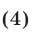
Решение:
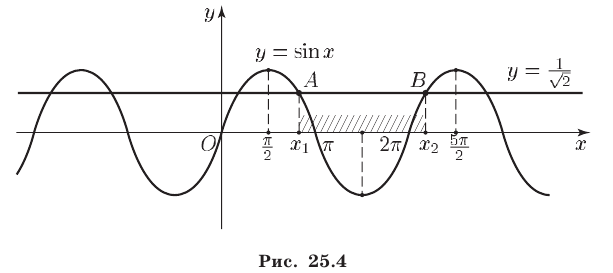
Первый способ. Построим графики функций 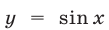 и
и 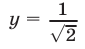 (рис. 25.4). Функция
(рис. 25.4). Функция 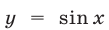 является периодической с периодом
является периодической с периодом 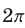 . Поэтому достаточно найти решения неравенства (4) на отрезке длиной
. Поэтому достаточно найти решения неравенства (4) на отрезке длиной 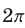 . В качестве такого отрезка выберем отрезок
. В качестве такого отрезка выберем отрезок 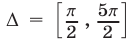 . На этом отрезке прямая
. На этом отрезке прямая 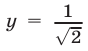 пересекает график функции
пересекает график функции 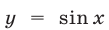 в точках
в точках 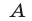 и
и 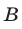 , абсциссы
, абсциссы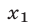 и
и 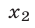 которых равны
которых равны 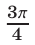 и
и 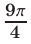 соответственно. Из рис. 25.4 видно, что решениями неравенства (4) на отрезке
соответственно. Из рис. 25.4 видно, что решениями неравенства (4) на отрезке  являются все числа интервала
являются все числа интервала
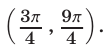 Поэтому множество всех решений неравенства (4) — это объединение интервалов вида
Поэтому множество всех решений неравенства (4) — это объединение интервалов вида
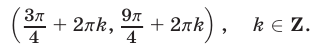
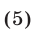
Ответ. 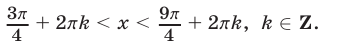
Второй способ. Построим единичную окружность и проведем через точку оси 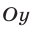 с ординатой
с ординатой 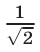 прямую
прямую 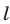 , параллельную оси
, параллельную оси 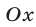 (см. рис. 25.5).
(см. рис. 25.5).
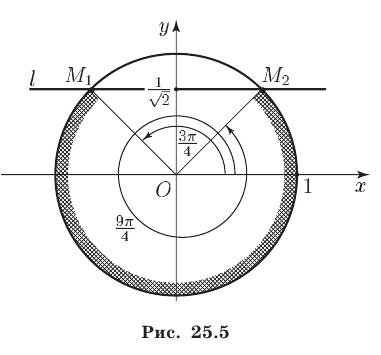
Прямая 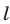 пересекает единичную окружность в точках
пересекает единичную окружность в точках 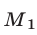 и
и 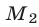
Точке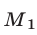 соответствует угол в
соответствует угол в 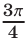 радиан, а точке
радиан, а точке 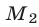 — угол в
— угол в 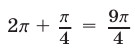 радиан. Из рис. 25.5 видно, что все точки единичной окружности, расположенные ниже прямой
радиан. Из рис. 25.5 видно, что все точки единичной окружности, расположенные ниже прямой 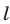 , имеют ординату, меньшую
, имеют ординату, меньшую 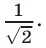
Итак, множество всех решений неравенства (4) представляет собой совокупность интервалов вида (5).
Пример №306.
Решить неравенство
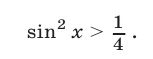
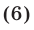
Решение:
Неравенство (6) равносильно неравенству
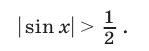
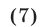
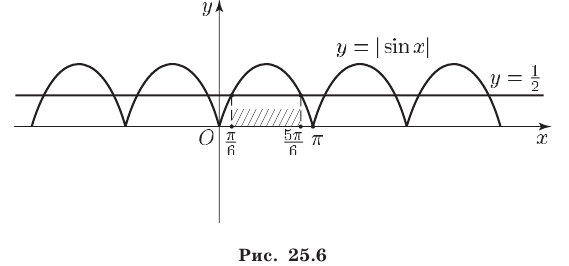
Построим график функции 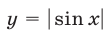 и проведем прямую
и проведем прямую 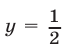 (рис. 25.6). Функция
(рис. 25.6). Функция 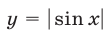 является периодической с периодом
является периодической с периодом 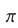 , а на отрезке
, а на отрезке 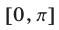 уравнение
уравнение 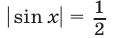 имеет корни
имеет корни 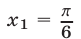 и
и 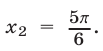 Из рис. 25.6 видно, что решениями неравенства (7) на отрезке
Из рис. 25.6 видно, что решениями неравенства (7) на отрезке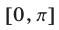 являются все числа из интервала
являются все числа из интервала 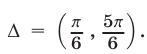 Множество решений неравенства (7) — это объединение интервалов, каждый из которых можно получить сдвигом интервала
Множество решений неравенства (7) — это объединение интервалов, каждый из которых можно получить сдвигом интервала  по оси
по оси 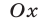 на
на 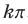 , где
, где 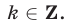
Ответ. 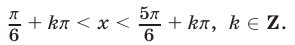
Пример №307.
Решить неравенство
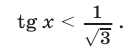
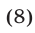
Решение:
Функция 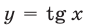 является периодической с периодом
является периодической с периодом 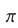 . Построим график функции
. Построим график функции 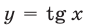 : на интервале
: на интервале 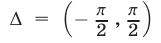 и проведем прямую
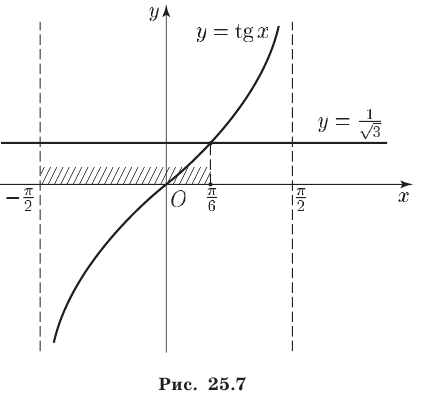
и проведем прямую 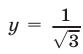 (см. рис. 25.7). Функция
(см. рис. 25.7). Функция 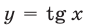 возрастает на интервале
возрастает на интервале  , а прямая
, а прямая 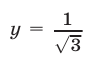 пересекает график этой функции в точке с абсциссой
пересекает график этой функции в точке с абсциссой 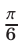 .
.
Поэтому решениями неравенства (8) на интервале  являются все числа
являются все числа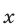 из интервала
из интервала 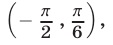 а множество всех решении неравенства (8) представляет собой совокупность интервалов вида
а множество всех решении неравенства (8) представляет собой совокупность интервалов вида
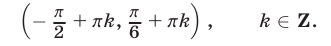
Ответ. 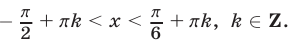
Пример №308.
Решить неравенство
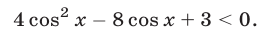
Решение:
Полагая 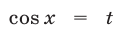 , получаем квадратное неравенство
, получаем квадратное неравенство 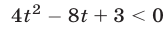 , равносильное неравенству
, равносильное неравенству 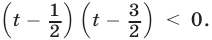
Поэтому неравенство (9) равносильно каждому из неравенств
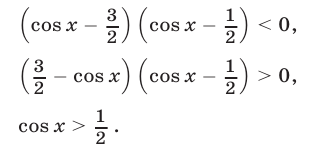
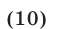
На отрезке 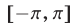 уравнение
уравнение 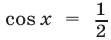 имеет корни
имеет корни 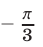 и
и 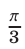 (см. рис. 25.1), а решениями неравенства (10) на этом отрезке являются все числа из интервала
(см. рис. 25.1), а решениями неравенства (10) на этом отрезке являются все числа из интервала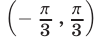 .
.
Множество решений неравенства (10) и равносильного ему неравенства (9) представляет собой объединение интервалов вида
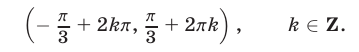
Ответ.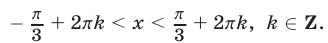
Пример №309.
Решить неравенство
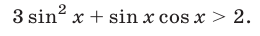
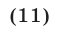
Решение:
Первый способ. Используя тождество 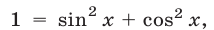 заменим неравенство (11) равносильным ему:
заменим неравенство (11) равносильным ему:
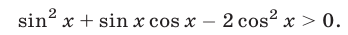
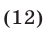
Как и при решении однородных тригонометрических уравнений, сведем неравенство (12) к квадратному относительно 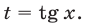 Рассмотрим два возможных случая:
Рассмотрим два возможных случая: 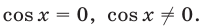
1) Пусть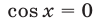 , тогда
, тогда 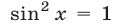 и неравенство (12) примет вид
и неравенство (12) примет вид 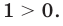 Следовательно, все значения
Следовательно, все значения 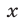 , удовлетворяющие уравнению
, удовлетворяющие уравнению 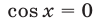 , т. е. числа
, т. е. числа
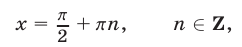
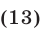
являются решениями неравенства (12).
2) Пусть 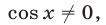 тогда
тогда 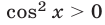 и неравенство (12) равносильно каждому из неравенств
и неравенство (12) равносильно каждому из неравенств
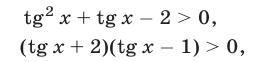
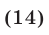
а неравенство (14) равносильно совокупности неравенств
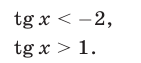
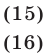
На интервале 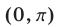 решения неравенства (15) — это все числа из интервала
решения неравенства (15) — это все числа из интервала  , а решения неравенства (16) все числа из интервала
, а решения неравенства (16) все числа из интервала 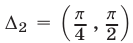 Следовательно, на интервале
Следовательно, на интервале 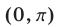 решениями неравенства (12), равносильного (11), являются все числа из интервалов
решениями неравенства (12), равносильного (11), являются все числа из интервалов 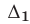 и
и 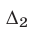 , а также число
, а также число 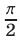 , т. е. все числа , принадлежащие интервалу
, т. е. все числа , принадлежащие интервалу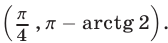
Так как функция 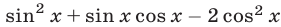 периодическая с периодом
периодическая с периодом 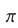 , то множество всех решений неравенства (12) представляет собой совокупность интервалов вида
, то множество всех решений неравенства (12) представляет собой совокупность интервалов вида 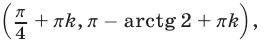
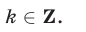
Ответ.
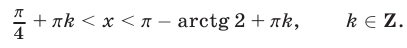
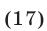
Второй способ. Неравенство (11) равносильно каждому из следующих неравенств:
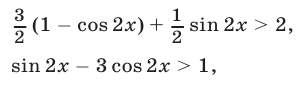
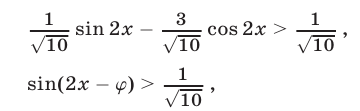
где 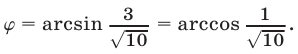 Отсюда находим
Отсюда находим
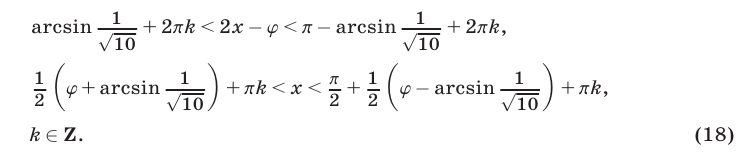
Заметим, что
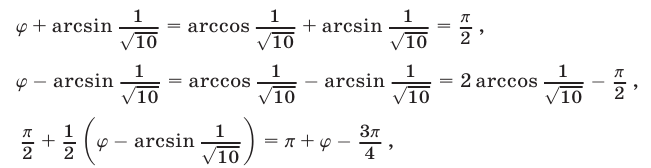
где 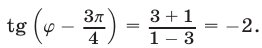 Поэтому двойное неравенство (18) но записать в виде (17).
Поэтому двойное неравенство (18) но записать в виде (17).
Пример №310.
Решить неравенство
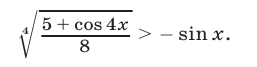
Решение:
Найдем решения неравенства на отрезке длиной 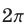 . Все значения
. Все значения 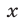 из интервала
из интервала 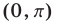 — решения неравенства, так как
— решения неравенства, так как 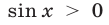 при
при 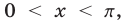 а левая часть неравенства определена и неотрицательна при всех
а левая часть неравенства определена и неотрицательна при всех 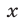 .
.
Пусть 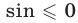 , тогда исходное неравенство равносильно каждому из неравенств
, тогда исходное неравенство равносильно каждому из неравенств
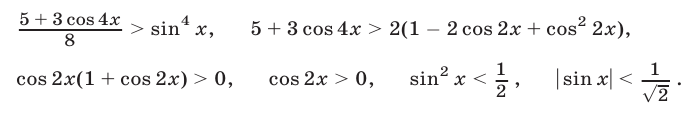
Так как 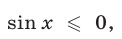 то
то 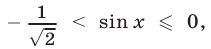 откуда
откуда 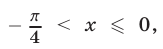
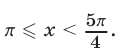
Итак, на отрезке 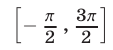 , решениями исходного неравенства являются все числа из интервала
, решениями исходного неравенства являются все числа из интервала 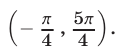
Ответ. 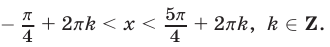
Пример №311.
Доказать, что если 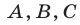 — углы треугольника, то
— углы треугольника, то
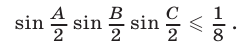
Решение:
Обозначим левую часть неравенства (19) через 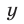 и выразим произведение синусов через разность косинусов. Тогда получим
и выразим произведение синусов через разность косинусов. Тогда получим
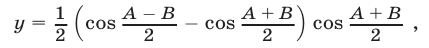
так как 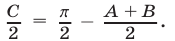 Полагая
Полагая 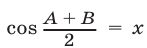 и применяя метод выделения полного квадрата, имеем
и применяя метод выделения полного квадрата, имеем
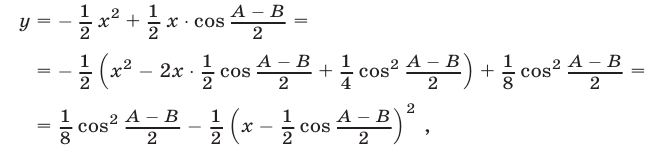
откуда следует, что
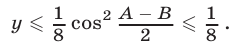
Неравенство (19) доказано.
Пример №312.
Доказать, что если 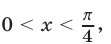 то верно неравенство
то верно неравенство
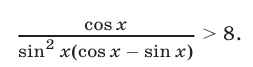
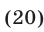
Решение:
Так как 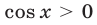 при
при 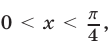 то, разделив числитель и знаменатель левой части неравенства (20) на
то, разделив числитель и знаменатель левой части неравенства (20) на 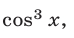 получим равносильное ему неравенство 1
получим равносильное ему неравенство 1
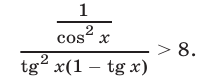
Обозначим левую часть неравенства (21) через 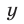 и воспользуемся формулой
и воспользуемся формулой 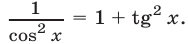 Тогда задача сведется к доказатель- ству неравенства
Тогда задача сведется к доказатель- ству неравенства
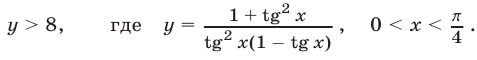
Полагая 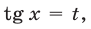 получаем
получаем 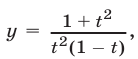 где
где 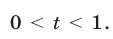 Заметим, что
Заметим, что
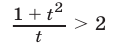 при
при 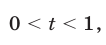
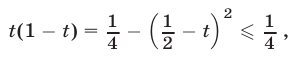
и поэтому
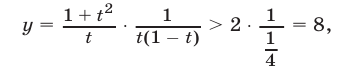
т. е. 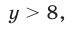 что и требовалось доказать.
что и требовалось доказать.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

